题目内容
在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.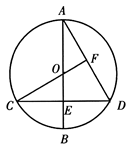
60°
解析试题分析:连接BD,先根据圆周角定理证得BD⊥AD,再结合CF⊥AD可得BD∥CF,即可得到∠BDC=∠C,再根据圆周角定理可得∠C=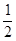 ∠BOC,最后根据三角形的内角和定理求解即可.
∠BOC,最后根据三角形的内角和定理求解即可.
连接BD 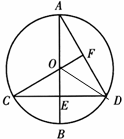
∵AB是⊙O的直径
∴BD⊥AD
又∵CF⊥AD
∴BD∥CF
∴∠BDC=∠C
又∵∠BDC=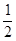 ∠BOC
∠BOC
∴∠C=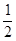 ∠BOC
∠BOC
∵AB⊥CD
∴∠C=30°
∴∠ADC=60°.
考点:圆周角定理,平行线的判定和性质,三角形的内角和定理
点评:解题的关键是熟练掌握直径所对的圆周角是直角;同弧所对的圆周角相等,都等于所对圆心角的一半.

练习册系列答案
相关题目
 22、如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
22、如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°. 直线AB相交于点G.
直线AB相交于点G.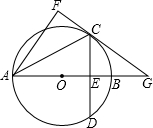 C与直线AB相交于点G.
C与直线AB相交于点G. 如图,在⊙O中,直径AB⊥弦CD于E,连接BD,若∠D=30°,BD=2,则AE的长为( )
如图,在⊙O中,直径AB⊥弦CD于E,连接BD,若∠D=30°,BD=2,则AE的长为( )