题目内容

如图，已知二次函数y=ax2+2x+c的图象与y轴相交于点M（0，8），与x轴的一个交点为N精英家教网（4，0）．
（1）求a，c的值；
（2）结合图象，写出x为负数时，函数值y的取值范围．
分析：（1）将点M（0，8），N（4，0）代入y=ax2+2x+c求得a、c即可；
（2）由图象可知，当x为负数时，y的值应小于8．
解答：解：（1）依题意
8=c
0=a
×42+2×4+c（3分），
解得
a=-1
c=8
（4分）

（2）由图象知，x为负数（或x＜0）时，y随x的增大而增大（5分），
所以，函数值y的取值范围是y＜8（7分）．
点评：本题考查了抛物线与x轴的交点问题，以及观察图象知信息的能力，难度较大．
练习册系列答案
相关题目
如图，已知二次函数图象的顶点坐标为C（1，1），直线y=kx+m的图象与该二次函数的图象交于A、B两点，其中A点坐标为（
5
2
，
13
4
），B点在y轴上，直线与x轴的交点为F，P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于E点．
（1）求k，m的值及这个二次函数的解析式；
（2）设线段PE的长为h，点P的横坐标为x，求h与x之间的函数关系式，并写出自变量x的取值范围；
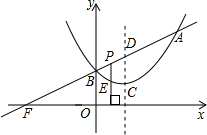（3）D为直线AB与这个二次函数图象对称轴的交点，在线段AB上是否存在点P，使得以点P、E、D为顶点的精英家教网三角形与△BOF相似？若存在，请求出P点的坐标；若不存在，请说明理由．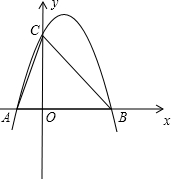
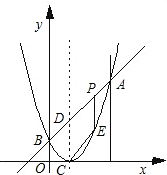如图，已知二次函数y=ax2+bx+3（a≠0）的图象与x轴交于点A（-1，0）和点B（3，0）两点（点A在点B的左边），与y轴交于点C．
（1）求此二次函数的解析式，并写出它的对称轴；
（2）若直线l：y=kx（k＞0）与线段BC交于点D（不与点B，C重合），则是否存在这样的直线l，使得以B，O，D为顶点的三角形与△BAC相似？若存在，求出点D的坐标；若不存在，请说明理由；
（3）若直线l′：y=m与该抛物线交于M、N两点，且以MN为直径的圆与x轴相切，求该圆半径的长度．
精英家教网
精英家教网如图，已知二次函数图象的顶点坐标为C（1，0），直线y=x+b与该二次函数的图象交于A、B两点，其中点A的坐标为（3，4），点B在y轴上．点P为线段AB上的一个动点（点P与A、B不重合），过点P作x轴的垂线与该二次函数的图象交于点E．
（1）求b的值及这个二次函数的关系式；
（2）设线段PE的长为h，点P的横坐标为x，求h与x之间的函数关系式，并写出自变量x的取值范围；
（3）若点D为直线AB与该二次函数的图象对称轴的交点，则四边形DCEP能否构成平行四边形？如果能，请求出此时P点的坐标；如果不能，请说明理由．
（4）以PE为直径的圆能否与y轴相切？如果能，请求出点P的坐标；如果不能，请说明理由．
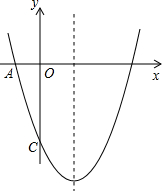精英家教网如图，已知二次函数y=ax2-4x+c的图象与坐标轴交于点A（-1，0）和点C（0，-5）．
（1）求该二次函数的解析式和它与x轴的另一个交点B的坐标．
（2）在上面所求二次函数的对称轴上存在一点P（2，-2），连接OP，找出x轴上所有点M的坐标，使得△OPM是等腰三角形．
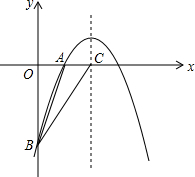（2012•衡水一模）如图，已知二次函数y=-
12
x2+bx+c的图象经过A（2，0）、B（0，-6）两点．
（1）求这个二次函数的解析式；
（2）设该二次函数图象的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积；
（3）若抛物线的顶点为D，在y轴上是否存在一点P，使得△PAD的周长最小？若存在，求出点P的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网