题目内容
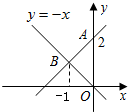如图，一次函数图象与y轴交于点A，且与正比例函数y=-x的图象交于点B，则该一次函数图象与x轴的交点为（ ）| A、（0，-2） | B、（-2，0） | C、（-1，0） | D、（-3，0） |
分析：将x=-1代入y=-x中可求B点纵坐标为1，设一次函数关系式y=kx+b，将A（0，2），B（-1，1）代入可求一次函数关系式，从而可求一次函数图象与x轴的交点．
解答：解：把x=-1代入y=-x中，得y=1，即B（-1，1），
设一次函数关系式y=kx+b，
将A（0，2），B（-1，1）得
，解得
，
∴y=x+2，
令y=0，得x=-2，即一次函数与x轴的交点坐标为（-2，0）．
故选B．
设一次函数关系式y=kx+b，
将A（0，2），B（-1，1）得
|
|
∴y=x+2，
令y=0，得x=-2，即一次函数与x轴的交点坐标为（-2，0）．
故选B．
点评：本题考查了求两直线交点坐标的问题．关键是利用已知直线解析式求交点坐标，代入所求直线解析式．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
如图，一次函数图象与x轴相交于点B，与反比例函数图象相交于点A（1，-6）；△AOB的面积为6．求一次函数和反比例函数的解析式．
（2012•重庆模拟）如图，一次函数图象与反比例函数图象交于A、B两点，与x轴交于点C，与y轴交于点D，OC=1，tan∠DCO=2，已知点A纵坐标为-2．
（2011•西双版纳）如图，反比例函数
如图，一次函数经过点A（2，3），B（-1，6）．求：