题目内容
小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
| 时刻 | 12:00 | 13:00 | 14:30 |
| 碑上的数 | 是一个两位数,数字之和为6 | 十位与个位数字与12:00时所看到的正好颠倒了 | 比12:00时看到的两位数中间多了个0 |
- A.24
- B.42
- C.51
- D.15
D
分析:设小明12时看到的两位数,十位数为x,个位数为y,根据两位数之和为6可列一个方程,再根据匀速行驶,12-13时行驶的里程数等于13-14:30时行驶的里程数除以1.5列出第二个方程,解方程组即可.
解答:设小明12时看到的两位数,十位数为x,个位数为y,即为10x+y;
则13时看到的两位数为x+10y,12-13时行驶的里程数为:(10y+x)-(10x+y);
则14:30时看到的数为100x+y,14:30时-13时行驶的里程数为:(100x+y)-(10y+x);
由题意列方程组得:
 ,
,
解得: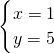 ,
,
所以12:00时看到的两位数是15,
故选D.
点评:本题考查了数学在生活中的运用,及二元一次方程组的解法.正确理解题意并列出方程组是解题的关键.
分析:设小明12时看到的两位数,十位数为x,个位数为y,根据两位数之和为6可列一个方程,再根据匀速行驶,12-13时行驶的里程数等于13-14:30时行驶的里程数除以1.5列出第二个方程,解方程组即可.
解答:设小明12时看到的两位数,十位数为x,个位数为y,即为10x+y;
则13时看到的两位数为x+10y,12-13时行驶的里程数为:(10y+x)-(10x+y);
则14:30时看到的数为100x+y,14:30时-13时行驶的里程数为:(100x+y)-(10y+x);
由题意列方程组得:
 ,
,解得:
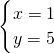 ,
,所以12:00时看到的两位数是15,
故选D.
点评:本题考查了数学在生活中的运用,及二元一次方程组的解法.正确理解题意并列出方程组是解题的关键.

练习册系列答案
相关题目
小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
则12:00时看到的两位数是( )
| 时刻 | 12:00 | 13:00 | 14:30 |
| 碑上的数 | 是一个两位数,数字之和为6 | 十位与个位数字与12:00时所看到的正好颠倒了 | 比12:00时看到的两位数中间多了个0 |
| A、24 | B、42 | C、51 | D、15 |
“小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
| 时刻 | 12:00 | 13:00 | 14:30 |
| 碑上的数 | 是一个两位数,数字之和为6 | 十位与个位数字与12:00时所看到的正好颠倒了 | 比12:00时看到的两位数中间多了个0 |
“小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:
|
时刻 |
12:00 |
13:00 |
14:30 |
|
碑上的数 |
是一个两位数,数字之和为6 |
十位与个位数字与12:00时所看到的正好颠倒了 |
比12:00时看到的两位数中间多了个0 |
则12:00时看到的两位数是多少?
