题目内容
 某汽车客运公司规定旅客可以随身携带一定重量的行李,如果超过规定的重量,则需要购买行李票,行李票费用y(元)与行李重量x(千克)之间函数关系的图象如图所示.(1)求y与x之间的函数关系.(2)旅客最多可以免费携带多少千克的行李?
某汽车客运公司规定旅客可以随身携带一定重量的行李,如果超过规定的重量,则需要购买行李票,行李票费用y(元)与行李重量x(千克)之间函数关系的图象如图所示.(1)求y与x之间的函数关系.(2)旅客最多可以免费携带多少千克的行李?分析:(1)由图,已知两点,可根据待定系数法列方程,求函数关系式;
(2)旅客可免费携带行李,即y=0,代入由(1)求得的函数关系式,即可知质量为多少.
(2)旅客可免费携带行李,即y=0,代入由(1)求得的函数关系式,即可知质量为多少.
解答:解:(1)设一次函数y=kx+b,
∵当x=60时,y=6,当x=90时,y=10,
∴
解之,得
,
∴所求函数关系式为y=
x-2(x≥15);
(2)当y=0时,
x-2=0,所以x=15,
故旅客最多可免费携带15kg行李.
∵当x=60时,y=6,当x=90时,y=10,
∴
|
|
∴所求函数关系式为y=
| 2 |
| 15 |
(2)当y=0时,
| 2 |
| 15 |
故旅客最多可免费携带15kg行李.
点评:本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.注意自变量的取值范围不能遗漏.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 要购买行李票,行李票费用y(元)是行李质量x(kg)的一次函数.
要购买行李票,行李票费用y(元)是行李质量x(kg)的一次函数.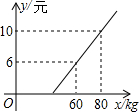 李票,行李票费用y(元)是行李重量x(千克)的一次函数,其图象如图.
李票,行李票费用y(元)是行李重量x(千克)的一次函数,其图象如图. 某长途汽车客运公司规定旅客可免费随身携带一定质量的行李,如果超过规定的质量,则需购买行李票.行李费用y(元)是行李质量x(千克)的一次函数,其图象如图所示.旅客最多可免费携带行李的质量是
某长途汽车客运公司规定旅客可免费随身携带一定质量的行李,如果超过规定的质量,则需购买行李票.行李费用y(元)是行李质量x(千克)的一次函数,其图象如图所示.旅客最多可免费携带行李的质量是