题目内容
 如图在反比例函数y=-
如图在反比例函数y=-| 2 |
| x |
| 3 |
| x |
| OA |
| OB |
| ||
| 3 |
| ||
| 3 |
分析:AB交y轴于C点,先设B点坐标为(a,
),利用AB∥x轴可表示出A点坐标为(-
,
),由于OA⊥OB得到∠AOB=90°,易证得Rt△AOC∽Rt△OBC,则
=
=
,即
=
=
,利用后面的等式可解出a2=
,于是得到
=
=
=
.
| 3 |
| a |
| 2a |
| 3 |
| 3 |
| a |
| OA |
| OB |
| OC |
| BC |
| AC |
| OC |
| OA |
| OB |
| ||
| a |
| ||
|
3
| ||
| 2 |
| OA |
| OB |
| ||
| a |
| 3 |
| a2 |
| 3 | ||||
|
| ||
| 3 |
解答:解:AB交y轴于C点,如图,
设B点坐标为(a,
),
∵AB∥x轴,
∴A点的纵坐标为
,OC⊥AB,
把y=
代入y=-
得x=-
,则A点坐标为(-
,
),
∵OA⊥OB,
∴∠AOB=90°,
∴Rt△AOC∽Rt△OBC,
∴
=
=
,即
=
=
,
由
=
得a4=
,
∴a2=
,
∴即
=
=
=
.
故答案为
.

设B点坐标为(a,
| 3 |
| a |
∵AB∥x轴,
∴A点的纵坐标为
| 3 |
| a |
把y=
| 3 |
| a |
| 2 |
| x |
| 2a |
| 3 |
| 2a |
| 3 |
| 3 |
| a |
∵OA⊥OB,
∴∠AOB=90°,
∴Rt△AOC∽Rt△OBC,
∴
| OA |
| OB |
| OC |
| BC |
| AC |
| OC |
| OA |
| OB |
| ||
| a |
| ||
|
由
| ||
| a |
| ||
|
| 27 |
| 2 |
∴a2=
3
| ||
| 2 |
∴即
| OA |
| OB |
| ||
| a |
| 3 |
| a2 |
| 3 | ||||
|
| ||
| 3 |
故答案为
| ||
| 3 |
点评:本题考查了反比例函数的综合题:反比例函数图象上的点的坐标满足其解析式;利用相似三角形的相似比进行几何计算是常用的方法.

练习册系列答案
相关题目
 如图在反比例函数y=-
如图在反比例函数y=-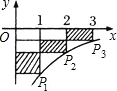 (1)如图在反比例函数y=
(1)如图在反比例函数y= (x>0)的图象上,有三点P1、P2、P3,它们的横坐标依次为1、2、3,分别过这3个点作x轴、y轴的垂线,设图中阴影部分面积依次为S1、S2、S3,则S1+S2+S3=______.
(x>0)的图象上,有三点P1、P2、P3,它们的横坐标依次为1、2、3,分别过这3个点作x轴、y轴的垂线,设图中阴影部分面积依次为S1、S2、S3,则S1+S2+S3=______. (x>0)的图象有交点,求m的取值范围.
(x>0)的图象有交点,求m的取值范围.
 (x>0)的图象上有三点P1、P2、P3,它们的横坐标依次为1,2,3,分别过这3个点作x轴y轴的垂线,设图中阴影部分面积依次为S1、S2、S3,则S1+S2+S3= .
(x>0)的图象上有三点P1、P2、P3,它们的横坐标依次为1,2,3,分别过这3个点作x轴y轴的垂线,设图中阴影部分面积依次为S1、S2、S3,则S1+S2+S3= .