题目内容
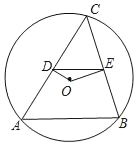
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,4)、D(3,0).
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COB的面积相等.求点P的坐标.
【答案】(1)y=﹣![]() ;(2)点P的坐标为(
;(2)点P的坐标为(![]() ,﹣20),(﹣
,﹣20),(﹣![]() ,20).
,20).
【解析】
(1)根据菱形的性质可得菱形的边长,进而可得点C的坐标,代入反比例函数解析式可得所求的解析式;(2)设出点P的坐标,易得△COB的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,继而可求得点P的坐标.
(1)由题意知,OA=4,OD=3
在Rt△AOB中,AD=![]() =5,
=5,
∵四边形ABCD为菱形,
∴AD=BC=AB=CD=5,
∴C(3,﹣5).
设经过点C的反比例函数的解析式为y=![]() (k≠0),
(k≠0),
则![]() =﹣5,
=﹣5,
解得:k=﹣15.
故所求的反比例函数的解析式为y=﹣![]() ;
;
(2)设P(x,y)
∵AD=AB=5,OA=4,
∴OB=1,S△COB=![]() ×1×3=
×1×3=![]() ,
,
即![]() ×OA×|x|=
×OA×|x|=![]() ,
,
∴|x|=![]() ,
,
∴x=±![]() ,
,
此时y=±20,
故点P的坐标为(![]() ,﹣20),(﹣
,﹣20),(﹣![]() ,20).
,20).

 天天向上口算本系列答案
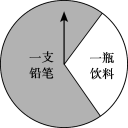
天天向上口算本系列答案【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.