Question

【题目】在△ABC中，∠ACB＝90°．

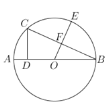
（1）作出经过点B，圆心O在斜边AB上且与边AC相切于点E的⊙O（要求：尺规作图，保留作图痕迹，不写作法和证明）．

（2）设（1）中所作的⊙O与边AB交于异于点B的另外一点D，若⊙O得直径为5，BC＝4，求AD的长度．（如果尺规作图画不出图形，此小题可画草图解答）

Answer 1

【答案】（1）详见解析；（2）．

【解析】

（1）先作∠ABC的平分线BE，再过点E作OE⊥AC交AB于O点，则利用角平分线的性质和平行线的性质可证明EO＝OB，然后以O点为圆心，OB为半径作圆满足条件；

（2）利用切线的性质得到OE⊥AC，则OE∥BC，于是可证明△AOE∽△ABC，利用相似比可计算出AB＝，然后计算AB﹣BD即可．

（1）如图，⊙O为所作；

（2）∵AB与⊙O相切于点E，

∴OE⊥AC，

∵∠C＝90°，

∴OE∥BC，

∴△AOE∽△ABC，

∴＝，即＝，解得AB＝，

∴AD＝AB﹣BD＝﹣5＝．