题目内容
如图，在△ABC中，DE∥BC，BD=2AD，设| AB |
| a |
| AC |
| b |
| a |
| b |
| DE |
考点：*平面向量
专题：
分析：首先利用三角形法则，可求得
，然后由在△ABC中，DE∥BC，可求得△ADE∽△ABC，又由BD=2AD，即可求得答案．
| BC |
解答：解：∵
=
，
=
，
∴
=
-
=
-
，
∵在△ABC中，DE∥BC，
∴△ADE∽△ABC，
∴
=
，
∵BD=2AD，
∴DE=
BC，
∴
=
-
．
故答案为：
-
．
| AB |
| a |
| AC |
| b |
∴
| BC |
| AC |
| AB |
| b |
| a |
∵在△ABC中，DE∥BC，
∴△ADE∽△ABC，
∴
| DE |
| BC |
| AD |
| AB |
∵BD=2AD，
∴DE=
| 1 |
| 3 |
∴
| DE |
| 1 |
| 3 |
| b |
| 1 |
| 3 |
| a |
故答案为：
| 1 |
| 3 |
| b |
| 1 |
| 3 |
| a |
点评：此题考查了平面向量的知识与相似三角形的判定与性质．此题难度不大，注意掌握三角形法则的应用，注意掌握数形结合思想的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
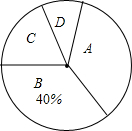为了了解我校九年级男生立定跳远的成绩，从全校随机抽50名男生的测试成绩进行调查．根据测试评分标准，将他们的得分按优秀、良好、及格、不及格（分别用A、B、C、D表示）四个等级进行统计，并绘制成统计表和扇形图，如图：
如图所示，已知菱形OABC，点C在x轴正半轴上，直线y=x经过一象限内点A，菱形OABC的面积等于