题目内容
【题目】如图，在平面直角坐标系中，点M是第一象限内一点，过M的直线分别交x轴，y轴的正半轴于A，B两点，且M是AB的中点．以OM为直径的⊙P分别交x轴，y轴于C，D两点，交直线AB于点E（位于点M右下方），连结DE交OM于点K． 
（1）若点M的坐标为（3，4）， ①求A，B两点的坐标；
②求ME的长．
（2）若 
=3，求∠OBA的度数．
（3）设tan∠OBA=x（0＜x＜1）， =y，直接写出y关于x的函数解析式．
【答案】
（1）解：①连接DM、MC，如图1．
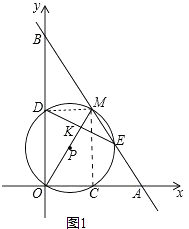
∵OM是⊙P的直径，
∴∠MDO=∠MCO=90°．
∵∠AOB=90°，
∴四边形OCMD是矩形，
∴MD∥OA，MC∥OB，
∴ 
， 
．
∵点M是AB的中点，即BM=AM，
∴BD=DO，AC=OC．
∵点M的坐标为（3，4），
∴OB=2OD=8，OA=2OC=6，
∴点B的坐标为（0，8），点A的坐标为（6，0）；
②在Rt△AOB中，OA=6，OB=8，
∴AB= 
=10．
∴BM= 
AB=5．
∵∠OBM=∠EBD，∠BOM=∠BED，
∴△OBM∽△EBD，
∴ 
= 
，
∴ 
= 
，
∴BE= 
，
∴ME=BE﹣BM= ﹣5= 
（2）解：连接DP、PE，如图2．
∵ 
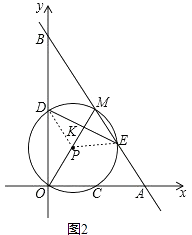
=3，
∴OK=3MK，
∴OM=4MK，PM=2MK，
∴PK=MK．
∵OD=BD，OP=MP，
∴DP∥BM，
∴∠PDK=∠MEK，∠DPK=∠EMK．
在△DPK和△EMK中，
，
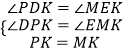∴△DPK≌△EMK，
∴DK=EK．
∵PD=PE，
∴PK⊥DE，
∴cos∠DPK= 
= ，
∴∠DPK=60°，
∴∠DOM=30°．
∵∠AOB=90°，AM=BM，
∴OM=BM，
∴∠OBA=∠DOM=30°
（3）解：y关于x的函数解析式为y= 
．
提示：连接PD、OE，如图3．
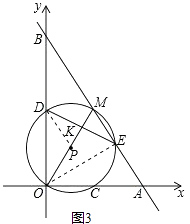
设MK=t，则有OK=yt，OM=（y+1）t，
BM=OM=（y+1）t，DP=PM= 
，
PK= ﹣t= 
．
由DP∥BM可得△DKP∽△EKM，
则有 
= 
，可得ME= 
t．
∵OM是⊙P的直径，
∴∠OEM=90°，
∴OE2=OM2﹣ME2=[（y+1）t]2﹣[ t]2= 
（y2﹣2y），
即OE= 
，
BE=BM+ME=（y+1）t+ t= 
，
∴x=tan∠OBA= 
= 
，
∴x2= 
=1﹣ 
，
整理得：y= ．
【解析】（1）①连接DM、MC，如图1，易证四边形OCMD是矩形，从而得到MD∥OA，MC∥OB，由点M是AB的中点即可得到BD=DO，AC=OC，然后利用点M的坐标就可解决问题；②根据勾股定理可求出AB的长，从而得到BM的长，要求ME的长，只需求BE的长，只需证△OBM∽△EBD，然后运用相似三角形的性质即可；（2）连接DP、PE，如图2，由 =3可得OK=3MK，进而得到OM=4MK，PM=2MK，PK=MK．易证△DPK≌△EMK，则有DK=EK．由PD=PE可得PK⊥DE，从而可得cos∠DPK= = ，则有∠DPK=60°，根据圆周角定理可得∠DOM=30°．由∠AOB=90°，AM=BM可得OM=BM，即可得到∠OBA=∠DOM=30°；（3）连接PD、OE，如图3，设MK=t，则有OK=yt，OM=（y+1）t，BM=OM=（y+1）t，DP=PM= ，PK= ．由DP∥BM可得△DKP∽△EKM，则有 = ，由此可得ME= t，从而可求得OE= ，BE= ，则有x=tan∠OBA= = ，即x2= =1﹣ ，整理得y= ．
【考点精析】通过灵活运用直角三角形斜边上的中线和勾股定理的概念，掌握直角三角形斜边上的中线等于斜边的一半；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．
