题目内容
【题目】如图，⊙P与y轴相切于坐标原点O（0，0），与x轴相交于点A（5，0），过点A的直线AB与y轴的正半轴交于点B，与⊙P交于点C． 
（1）已知AC=3，求点B的坐标；
（2）若AC=a，D是OB的中点．问：点O、P、C、D四点是否在同一圆上？请说明理由．如果这四点在同一圆上，记这个圆的圆心为O1 ， 函数 
的图象经过点O1 ， 求k的值（用含a的代数式表示）．
【答案】
（1）解：解法一：连接OC，
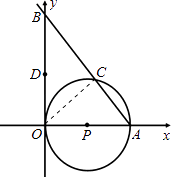
∵OA是⊙P的直径，
∴OC⊥AB，
在Rt△AOC中， 
，
在Rt△AOC和Rt△ABO中，
∵∠CAO=∠OAB
∴Rt△AOC∽Rt△ABO，
∴ 
，即 
，
∴ 
，
∴ 
解法二：连接OC，因为OA是⊙P的直径，
∴∠ACO=90°
在Rt△AOC中，AO=5，AC=3，
∴OC=4，
过C作CE⊥OA于点E，则： 
，
即： 
，
∴ 
，
∴ 
，
∴ 
，
设经过A、C两点的直线解析式为：y=kx+b．
把点A（5，0）、 代入上式得： 
，
解得：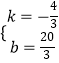 
，
∴ 
，
∴点
（2）解：点O、P、C、D四点在同一个圆上，理由如下：
连接CP、CD、DP，
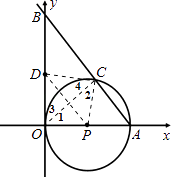
∵OC⊥AB，D为OB上的中点，
∴ 
，
∴∠3=∠4，
又∵OP=CP，
∴∠1=∠2，
∴∠1+∠3=∠2+∠4=90°，
∴PC⊥CD，又∵DO⊥OP，
∴Rt△PDO和Rt△PDC是同以PD为斜边的直角三角形，
∴PD上的中点到点O、P、C、D四点的距离相等，
∴点O、P、C、D在以DP为直径的同一个圆上；
由上可知，经过点O、P、C、D的圆心O1是DP的中点，圆心 
，
由（1）知：Rt△AOC∽Rt△ABO，
∴ 
，
求得：AB= 
，在Rt△ABO中， 
，
OD= 
， 
∴ 
，点O1在函数 
的图象上，
∴ 
，
∴ 
．
【解析】（1）此题有两种解法： 解法一：连接OC，根据OA是⊙P的直径，可得OC⊥AB，利用勾股定理求得OC，再求证Rt△AOC∽Rt△ABO，利用其对应变成比例求得OB即可；
解法二：连接OC，根据OA是⊙P的直径，可得∠ACO=90°，利用勾股定理求得OC，过C作CE⊥OA于点E，分别求得CE、0E，设经过A、C两点的直线解析式为：y=kx+b．把点A（5，0）、 代入上式解得即可．（2）连接CP、CD、DP，根据OC⊥AB，D为OB上的中点，可得 ，求证Rt△PDO和Rt△PDC是同以PD为斜边的直角三角形，可得PD上的中点到点O、P、C、D四点的距离相等，由上可知，经过点O、P、C、D的圆心O1是DP的中点，圆心 ，由（1）知：Rt△AOC∽Rt△ABO，可得 ，求得：AB、OD即可．
【考点精析】掌握直角三角形斜边上的中线和勾股定理的概念是解答本题的根本，需要知道直角三角形斜边上的中线等于斜边的一半；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
