题目内容
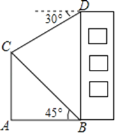
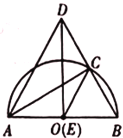
【题目】如图,已知![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() ,半径
,半径![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,点
,点![]() 的对应点为
的对应点为![]() ,当点
,当点![]() 与点
与点![]() 重合时停止.连接
重合时停止.连接![]() 并延长到点
并延长到点![]() ,使得
,使得![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() ______;
______;
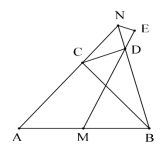
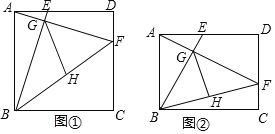
(2)如图,当点![]() 与点
与点![]() 重合时,判断
重合时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
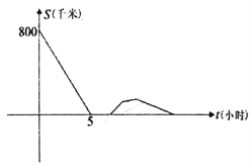
(3)如图,当![]() 时,求
时,求![]() 的长;
的长;

(4)如图,若点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,当
,当![]() 与半圆
与半圆![]() 相切时,直接写出直线
相切时,直接写出直线![]() 与
与![]() 的位置关系.
的位置关系.

【答案】(1)![]() ;(2)
;(2)![]() 是等边三角形,理由见解析;(3)
是等边三角形,理由见解析;(3)![]() 的长为
的长为![]() 或
或![]() ;(4)
;(4)![]()
【解析】
(1)先证AC垂直平分DB,即可证得AD=AB;
(2)先证AD=BD,又因为AD=AB,可得△ABD是等边三角形;
(3)分当点![]() 在
在![]() 上时和当点
上时和当点![]() 在
在![]() 上时,由勾股定理列方程求解即可;
上时,由勾股定理列方程求解即可;
(4)连结OC,证明OC∥AD, 由![]() 与半圆
与半圆![]() 相切,可得∠OCP=90°,即可得到
相切,可得∠OCP=90°,即可得到![]() 与
与![]() 的位置关系.
的位置关系.
解:(1)∵![]() 为直径,
为直径,
∴∠ACB=90°,
又∵![]()
∴AD=AB
∴![]() ,
,
故答案为10;
(2)![]() 是等边三角形,
是等边三角形,
理由如下:∵点![]() 与点
与点![]() 重合,∴
重合,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() 是等边三角形;
是等边三角形;
(3)∵![]() ,∴
,∴![]() ,
,
当点![]() 在
在![]() 上时,
上时,
则![]() ,
,![]() ,∵
,∵![]() ,
,![]() ,
,
∴在![]() 和
和![]() 中,
中,
由勾股定理得![]() ,即
,即![]() ,
,
解得![]() ,∴
,∴![]() ;
;
当点![]() 在
在![]() 上时,同理可得
上时,同理可得![]() ,
,
解得![]() ,∴
,∴![]() ,
,
综上所述,![]() 的长为
的长为![]() 或
或![]() ;
;
(4)![]() .
.
如图,连结OC,
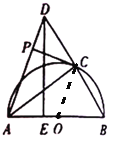
∵![]() 与半圆
与半圆![]() 相切,
相切,
∴OC⊥PC,
∵△ADB为等腰三角形,![]() ,
,
∴∠DAC=∠BAC,
∵AO=OC
∴∠CAO=∠ACO,
∴∠DAC=∠ACO,
∴OC∥AD,
∴![]() .
.

练习册系列答案
相关题目