题目内容
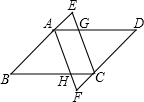（1998•河北）已知：如图，四边形ABCD为平行四边形，延长BA到E，延长DC到F，使BE=DF，AF交BC于H，CE交AD于G．求证：△AGE≌△CHF．
分析：由四边形ABCD是平行四边形可得到AB=CD，AB∥CD，因为=DF，所以AE=CF，因为AE∥CF，所以四边形AECF是平行四边形，所以可得到∠E=∠F，再证明∠EAG=∠FCH，由ASA即可证明：△AGE≌△CHF．
解答：证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
∵BE=DF，
∴AE=CF，
∵AE∥CF，
∴四边形AECF是平行四边形，
∴∠E=∠F，
又∵四边形ABCD是平行四边形，
∴∠BAD=∠BCD，
∴∠EAG=∠FCH，
∵在△AGE和△CHF中，
，
∴△AGE≌△CHF（ASA）．
∴AB=CD，AB∥CD，
∵BE=DF，
∴AE=CF，
∵AE∥CF，
∴四边形AECF是平行四边形，
∴∠E=∠F，
又∵四边形ABCD是平行四边形，
∴∠BAD=∠BCD，
∴∠EAG=∠FCH，
∵在△AGE和△CHF中，
|
∴△AGE≌△CHF（ASA）．
点评：本题考查了平行四边形的性质和判定、全等三角形的性质和判定，解题的关键是熟练掌握各种图形的判定方法和性质．
练习册系列答案
相关题目
（1998•河北）已知：如图弦AB经过⊙O的半径OC的中点P，且AP=2，PB=3，则是⊙O的半径等于（ ）
（1998•河北）已知：如图，在⊙O中，直径AB⊥CD，BE切⊙O于B，且BE=BC，CE交AB于F、交⊙O于M，连接MO并延长，交⊙O于N．则下列结论中，正确的是（ ）