题目内容
为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,二中学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间,根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:

(1)本次调查的学生人数是 人.
(2)图2中α是 度,并将图1条形统计图补充完整.
(3)请估算该校九年级学生自主学习的时间不少于1.5小时有 人.
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
(1)40;(2)54,补充图形如图; (3)330; (4)【解析】
图见解析.P(选中小亮)= 

【解析】
试题分析:(1)根据由自主学习的时间是1小时的人数占30%,可求得本次调查的学生人数;
(2) ,由自主学习的时间是0.5小时的人数为40×35%=14;(3)求出这40名学生自主学习时间不少于1.5小时的百分比乘以600即可;(4)根据题意画出树状图,然后由树状图求得所有等可能的结果与选中小亮A的情况,再利用概率公式求解即可求得答案.
,由自主学习的时间是0.5小时的人数为40×35%=14;(3)求出这40名学生自主学习时间不少于1.5小时的百分比乘以600即可;(4)根据题意画出树状图,然后由树状图求得所有等可能的结果与选中小亮A的情况,再利用概率公式求解即可求得答案.
试题解析:
【解析】
(1)∵自主学习的时间是1小时的有12人,占30%,∴12÷30%=40,故答案为:40; (2分)
(2) ,故答案为:54;自主学习的时间是0.5小时的人数为40×35%=14;补充图形如图:故答案为:54;
,故答案为:54;自主学习的时间是0.5小时的人数为40×35%=14;补充图形如图:故答案为:54;

(3)600× =330; (2分)故答案为:330;
=330; (2分)故答案为:330;
(4)画树状图得:

∵共有12种等可能的结果,选中小亮A的有6,
∴P(A)= . (2分)
. (2分)
考点:1.频数与频率;2.条形统计图;3.扇形统计图;4.用样本估计总体;5.简单事件的概率.

练习册系列答案
相关题目
 、
、 、
、 的最简公分母是 .
的最简公分母是 . .求CD和CE的长;
.求CD和CE的长; BF,求
BF,求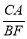 的值.
的值.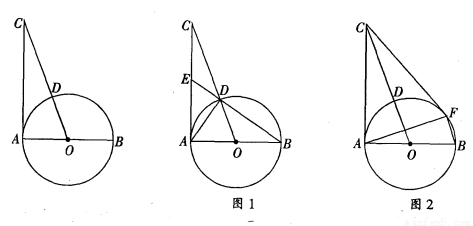

 C.3
C.3
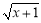 ,则自变量x的取值范围是( )
,则自变量x的取值范围是( )
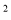 +bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)
+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)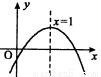
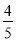 .下列结论:
.下列结论: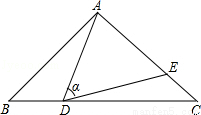
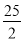 ;
; =±2 B.
=±2 B. =-6 C.
=-6 C. D.
D.