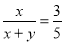题目内容
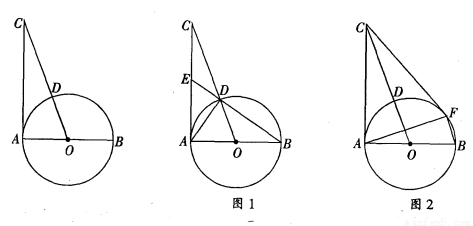
(本题满分12分)如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D.
(1)如图1,连接BD并延长BD交AC于点E,连接AD.
①证明:△CDE∽△CAD;
②若AB=2,AC=2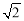 .求CD和CE的长;
.求CD和CE的长;
(2)如图2,过点C作⊙O的另一条切线,切点为F,连结AF、BF,若OC=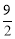 BF,求
BF,求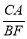 的值.
的值.
(1)①见解析;②CD=2;CE=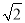
(2)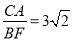
【解析】
试题分析:(1)①因为两个三角形有一公共角,所以只需要再证明一个角对应相等即可,根据条件AC是⊙O的切线,AB是⊙O的直径,利用互余的关系可证∠CAD=∠CDE;②在Rt△AOC中,由勾股定理可求OC=3,由△CDE∽△CAD,可得出CE= ;(2)设圆的半径为r,由△ABF∽△COA,得
;(2)设圆的半径为r,由△ABF∽△COA,得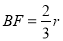 ,在Rt△COA中,由勾股定理可得CA=
,在Rt△COA中,由勾股定理可得CA=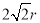 ,从而可得
,从而可得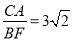 .
.
试题解析:(1)①证明:因为AC是⊙O的切线,所以∠1+∠BAD=90°,又因为AB是⊙O的直径,所以∠B+∠BAD=90°,所以∠1=∠B, 又OB=OD,所以∠2=∠B,又∠2=∠3,所以∠3=∠B,所以∠1=∠3,又∠C=∠C,所以△CDE∽△CAD;
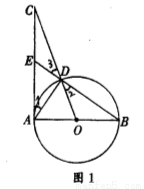
②在Rt△AOC中,OC=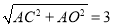 ,所以CD=OC-OD=3-1=2,又△CDE∽△CAD,所以
,所以CD=OC-OD=3-1=2,又△CDE∽△CAD,所以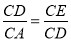 ,所以
,所以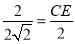 ,CE=
,CE= 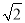 ;(2)设圆的半径为r,由△ABF∽△COA,,所以
;(2)设圆的半径为r,由△ABF∽△COA,,所以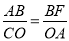 ,所以
,所以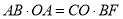 ,又OC=
,又OC=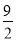 BF,AB=2r,OA=r,所以
BF,AB=2r,OA=r,所以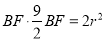 ,所以
,所以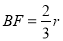 ,OC=3r,在Rt△COA中,由勾股定理可得CA=
,OC=3r,在Rt△COA中,由勾股定理可得CA=
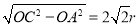 ,所以
,所以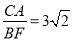 .
.
考点:1.切线的性质;2. 勾股定理;3.相似三角形的判定与性质.

练习册系列答案
相关题目
 中,自变量的取值范围是_________________.
中,自变量的取值范围是_________________.
 ,则∠BAC的度数为 °.
,则∠BAC的度数为 °.

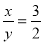 ,那么下列等式中,不一定正确的是( )
,那么下列等式中,不一定正确的是( )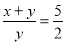 D.
D.