题目内容
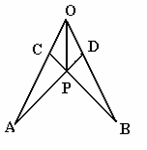
已知:如图,点B、C、E三点在同一条直线上,CD平分∠ACE, DB=DA,
DM⊥BE于M.
(1)求证:AC=BM+CM;
(2)若AC=2,BC=1,求CM的长.
(1)证明:

(1)证明:作DN⊥AC于N,
 ∵CD平分∠ACE,DM⊥BE
∵CD平分∠ACE,DM⊥BE
∴DN=DM ……………………1分
在Rt△DCN和Rt△DCM中,

∴Rt△DCN≌Rt△DCM(HL),
∴CN=CM, …………………………………2分
在Rt△ADN和Rt△BDM中,

∴Rt△ADN≌Rt△BDM(HL),
∴AN=BM,
∵AC=AN+CN
∴AC=BM+CM …………………………………3分
(2)解:∵AN=AC-CN, BM=BC+CM,
∴AC-CN=BC+CM
∴AC-CM=BC+CM
∴2CM=AC-BC, …………………………………4分
∵AC=2,BC=1,
∴CM=0.5 …………………………………5分

练习册系列答案
相关题目
 的方程
的方程 有三个根,且这三个根恰好可
有三个根,且这三个根恰好可 的取值范围是 .
的取值范围是 . 有意义的条件是( ).
有意义的条件是( ). B.
B. C.
C. D.
D.




 ,其中
,其中 .
.  形共有( ).
形共有( ).
