��Ŀ����
��֪ij�����ƻ��ÿ���302m3ľ��ΪijѧУ����500�����Σ�����У1250��ѧ��ʹ�ã��ó����������η�ΪA��B�����ͺţ��й��������£�
| �����ͺ� | һ����������ѧ����������λ���ˣ� | ����һ����������ľ | һ�����ε������ɱ�����λ��Ԫ�� | һ�����ε��˷ѣ���λ��Ԫ�� |
| A | 2 | 0.5 | 100 | 2 |
| B | 3 | 0.7 | 120 | 4 |
������A������x���ף�������ȫ�����β�������У���ܷ��ã��ܷ���=�����ɱ�+�˷ѣ�ΪyԪ��
��1����y��x֮��Ĺ�ϵʽ����ָ��x��ȡֵ��Χ��
��2�����ܷ���y��Сʱ������Ӧ��xֵ����ʱy��ֵ��
�⣺��1����������������x�ף��������������ε�������500��x���ף�
��������ã� ��
��
���������ʽ��ã�240��x��250��
�ܷ���y=��100+2��x+��120+4����500��x��=102x+62000��124x=��22x+62000��
��y=��22x+62000����240��x��250����
��2����y=��22x+62000����22��0��
��y��x�����������
�൱x=250ʱ���ܷ���yȡ����Сֵ��
��ʱ��������������250�ף���������250�ף������ܷ���y=��22��250+62000=56500Ԫ��

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д������������420ǧ�ף����ĸ��ٹ�·��ͨ���ڼס���������ʻ�ij�;���˳�ƽ���ٶ���ԭ����1.5���������Ӽص��ҵص�ʱ��������2Сʱ����ԭ����ƽ���ٶ�Ϊxǧ��/ʱ�����з���Ϊ��������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|
��6�ĵ����ǣ�������
| �� | A�� | ��6 | B�� | 6 | C�� |
| D�� |
|
 �ģ���λ��m3��
�ģ���λ��m3�� +
+ =2
=2 =2
=2 +
+ =
= �Ľ���ʽ��������ͼ����һ������B�����ꣻ
�Ľ���ʽ��������ͼ����һ������B�����ꣻ
 +|
+| ��1|+��
��1|+�� ����1��2sin45�㣻
����1��2sin45�㣻

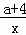 ��ͼ����ͼ��A��PΪ��ͼ���ϵĵ㣬�ҹ���ԭ������ĶԳƣ���PAB�У�PB��y�ᣬAB��x�ᣬPB��AB�ཻ�ڵ�B������PAB���������12�������x�ķ��̣�a��1��x2��x+
��ͼ����ͼ��A��PΪ��ͼ���ϵĵ㣬�ҹ���ԭ������ĶԳƣ���PAB�У�PB��y�ᣬAB��x�ᣬPB��AB�ཻ�ڵ�B������PAB���������12�������x�ķ��̣�a��1��x2��x+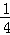 =0�ĸ��������������
=0�ĸ��������������