Question

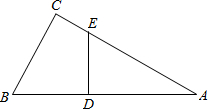如图，Rt△ABC中，∠C=90°，点D、E分别在AB、AC上，且DE⊥AB．若DE将ABC分成面积相等的两部分，且S_△ABC=20，AE=8，则AD=

（

26

+

6

）或（

26

-

6

）

．

Answer 1

分析：过点D作DF⊥AE于F，根据△ABC的面积求出△ADE的面积并求出DF的长度，再根据△ADF和△DFE相似，利用相似三角形对应边成比例列式求出AF，然后在Rt△ADF中，利用勾股定理列式求解即可得到AD的长度．

解答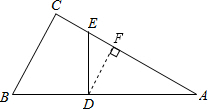：解：过点D作DF⊥AE于F，
∵S_△ABC=20，DE将ABC分成面积相等的两部分，
∴S_△ADE=

1

2

×20=10，
∵AE=8，

1

2

×8•DF=10，
解得DF=

5

2

，
∵DF⊥AE，DE⊥AB，
∴∠A+∠ADF=90°，∠ADF+∠EDF=90°，
∴∠A=∠EDF，
又∵∠ADF=∠DFE=90°，
∴△ADF∽△DFE，
∴

AF

DF

=

DF

EF

，
∴DF²=AF•EF，
即（

5

2

）²=AF•（8-AF），
整理得，4AF²-32AF+25=0，
解得AF=

8± 39

2

，
在Rt△ADF中，根据勾股定理，AD²=DF²+AF²，
代入数据得，AD²=（

5

2

）²+（

8± 39

2

）²=

25

4

+

103±16 39

4

，
=32±4

39

，
=26±2

156

+6，
=（

26

）²±2

26

×

6

+（

6

）²，
=（

26

±

6

）²，
所以，AD=（

26

+

6

）或（

26

-

6

）．
故答案为：（

26

+

6

）或（

26

-

6

）．

点评：本题考查了勾股定理，相似三角形的判定与性质，作出辅助线构造出Rt△ADF并利用相似三角形对应边成比例求出AF的长度是解题的关键．