题目内容
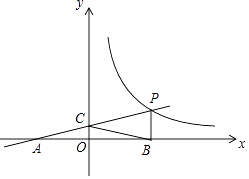
【题目】如图,OA⊥OB,AB⊥x轴于C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上.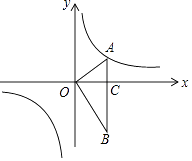
(1)求反比例函数y= ![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使S△AOP= ![]() S△AOB , 求点P的坐标.
S△AOB , 求点P的坐标.
【答案】
(1)
解:把A( ![]() ,1)代入反比例函数y=
,1)代入反比例函数y= ![]() 得:k=1×
得:k=1× ![]() =
= ![]() ,
,
所以反比例函数的表达式为y= ![]() ;
;
(2)
解:∵A( ![]() ,1),OA⊥AB,AB⊥x轴于C,
,1),OA⊥AB,AB⊥x轴于C,
∴OC= ![]() ,AC=1,
,AC=1,
OA= ![]() =
= ![]() =2,
=2,
∵tanA= ![]() =
= ![]() ,
,
∴∠A=60°,
∵OA⊥OB,
∴∠AOB=90°,
∴∠B=30°,
∴OB=2OC﹣2 ![]() ,
,
∴S△AOB= ![]() =
= ![]() =2
=2 ![]() ,
,
∵S△AOP= ![]() S△AOB,
S△AOB,
∴ ![]() ,
,
∵AC=1,
∴OP=2 ![]() ,
,
∴点P的坐标为(﹣2 ![]() ,0).
,0).
【解析】(1)把A的坐标代入反比例函数的解析式,即可求出答案;(2)求出∠A=60°,∠B=30°,求出线段OA和OB,求出△AOB的面积,根据已知S△AOP= ![]() S△AOB , 求出OP长,即可求出答案.
S△AOB , 求出OP长,即可求出答案.
【考点精析】关于本题考查的比例系数k的几何意义,需要了解几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能得出正确答案.

练习册系列答案
相关题目
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?