题目内容
如图,已知点C周围2180米范围内为原始森林保护区,在点A测得点C在 北偏东45°方向上,从点A向东走6000米到达点B,在点B测得C在北偏西60°方向上.
北偏东45°方向上,从点A向东走6000米到达点B,在点B测得C在北偏西60°方向上.
(1)求点C到直线AB的距离(结果保留根号);
(2)如果以AB为中轴线修一条宽为20米公路MN,那么公路MN会穿过原始森林保护区吗?说明理由.(
=1.732)
 北偏东45°方向上,从点A向东走6000米到达点B,在点B测得C在北偏西60°方向上.
北偏东45°方向上,从点A向东走6000米到达点B,在点B测得C在北偏西60°方向上.(1)求点C到直线AB的距离(结果保留根号);
(2)如果以AB为中轴线修一条宽为20米公路MN,那么公路MN会穿过原始森林保护区吗?说明理由.(
| 3 |
分析:(1)首先过点C作CD⊥AB于D,由已知得:∠EAC=45°,∠FBC=60°,EA⊥AB,FB⊥AB,AB=6000米,设CD=x米,利用三角函数的知识即可求得AD与BD的长,则可得方程:x+
x=6000,解此方程即可求得答案;
(2)由以AB为中轴线修一条宽为20米公路MN,即可求得点C到公路MN距离,与2180比较,即可求得答案.
| 3 |
(2)由以AB为中轴线修一条宽为20米公路MN,即可求得点C到公路MN距离,与2180比较,即可求得答案.
解答: 解:(1)过点C作CD⊥AB于D,
解:(1)过点C作CD⊥AB于D,
由已知得:∠EAC=45°,∠FBC=60°,EA⊥AB,FB⊥AB,AB=6000米,
∴∠CAD=90°-∠EAC=45°,∠CBD=90°-∠FBC=30°,
设CD=x米,
在Rt△ACD中,∠CAD=∠ACD=45°,
∴AD=CD=x米,
在Rt△BCD中,BD=
=
x(米),
∴x+
x=6000,
解得:x=3000
-3000(米);
∴点C到直线AB的距离为:3000
-3000米;
(2)公路MN不会穿过原始森林保护区.
理由:∵CD=3000
-3000=2196(米),
又∵以AB为中轴线修一条宽为20米公路MN,
∴点C到公路MN距离为:2196-10=2186(米),
∵2186>2180,
∴公路MN不会穿过原始森林保护区.
 解:(1)过点C作CD⊥AB于D,
解:(1)过点C作CD⊥AB于D,由已知得:∠EAC=45°,∠FBC=60°,EA⊥AB,FB⊥AB,AB=6000米,
∴∠CAD=90°-∠EAC=45°,∠CBD=90°-∠FBC=30°,
设CD=x米,
在Rt△ACD中,∠CAD=∠ACD=45°,
∴AD=CD=x米,
在Rt△BCD中,BD=
| CD |
| tan∠CBD |
| 3 |
∴x+
| 3 |
解得:x=3000
| 3 |
∴点C到直线AB的距离为:3000
| 3 |
(2)公路MN不会穿过原始森林保护区.
理由:∵CD=3000
| 3 |
又∵以AB为中轴线修一条宽为20米公路MN,
∴点C到公路MN距离为:2196-10=2186(米),
∵2186>2180,
∴公路MN不会穿过原始森林保护区.
点评:本题主要考查了方向角问题.此题难度适中,解题的关键是构造直角三角形,再解直角三角形,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 (2014•静安区一模)如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由.
(2014•静安区一模)如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由. ,已知
,已知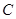 点周围200米范围内为原始森林保护区,在
点周围200米范围内为原始森林保护区,在 处测得
处测得 处,测得
处,测得 )
)
 北偏东45°方向上,从点A向东走6000米到达点B,在点B测得C在北偏西60°方向上.
北偏东45°方向上,从点A向东走6000米到达点B,在点B测得C在北偏西60°方向上.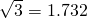 )
) )
)