题目内容
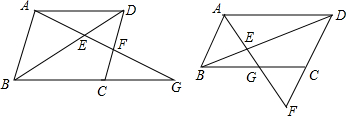 在?ABCD中,G为BC延长线上一点,射线AG与直线BD相交于E、与直线CD相交于F.
在?ABCD中,G为BC延长线上一点,射线AG与直线BD相交于E、与直线CD相交于F.
(1)求证: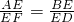 ;
;
(2)求证:AE2=EF•EG;
(3)如果把“G为BC延长线上一点”改为“G为线段BC上一点(不与点B、C重合)”,其它条件不变,(2)中的结论是否成立吗?若成立,请你加以证明;若不成立,请你说明理由.
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABE∽△FDE,
∴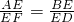 ;
;
(2)∵AD∥BC,
∴△ADE∽△GBE,
∴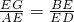 ,
,
∵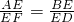 ,
,
∴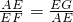 ,
,
∴AE2=EF•EG;
(3)结论AE2=EF•EG成立.
证明:在?ABCD中,AB∥CD,AD∥BC,
∴△ABE∽△FDE,△ADE∽△GBE,
∴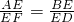 ,
,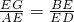 ,
,
∴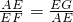 ,
,
∴AE2=EF•EG.
分析:(1)由四边形ABCD是平行四边形,可得AB∥CD,即可得△ABE∽△FDE,然后由相似三角形的对应边成比例,证得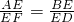 ;
;
(2)由AD∥BC,可得△ADE∽△GBE,然后由相似三角形的对应边成比例,可得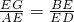 ,又由
,又由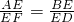 ,即可证得AE2=EF•EG;
,即可证得AE2=EF•EG;
(3)由在?ABCD中,AB∥CD,AD∥BC,可得△ABE∽△FDE,△ADE∽△GBE,然后由相似三角形的对应边成比例可得: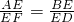 ,
,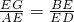 ,继而可证得AE2=EF•EG.
,继而可证得AE2=EF•EG.
点评:此题考查了相似三角形的判定与性质以及平行四边形的性质.此题难度适中,注意掌握数形结合思想的应用.
∴AB∥CD,AD∥BC,
∴△ABE∽△FDE,
∴
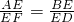 ;
;(2)∵AD∥BC,
∴△ADE∽△GBE,
∴
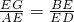 ,
,∵
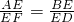 ,
,∴
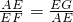 ,
,∴AE2=EF•EG;
(3)结论AE2=EF•EG成立.
证明:在?ABCD中,AB∥CD,AD∥BC,
∴△ABE∽△FDE,△ADE∽△GBE,
∴
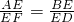 ,
,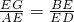 ,
,∴
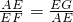 ,
,∴AE2=EF•EG.
分析:(1)由四边形ABCD是平行四边形,可得AB∥CD,即可得△ABE∽△FDE,然后由相似三角形的对应边成比例,证得
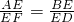 ;
;(2)由AD∥BC,可得△ADE∽△GBE,然后由相似三角形的对应边成比例,可得
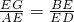 ,又由
,又由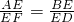 ,即可证得AE2=EF•EG;
,即可证得AE2=EF•EG;(3)由在?ABCD中,AB∥CD,AD∥BC,可得△ABE∽△FDE,△ADE∽△GBE,然后由相似三角形的对应边成比例可得:
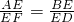 ,
,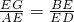 ,继而可证得AE2=EF•EG.
,继而可证得AE2=EF•EG.点评:此题考查了相似三角形的判定与性质以及平行四边形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
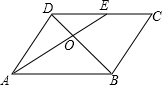 如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB等于( )cm2.
如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB等于( )cm2.| A、24 | B、36 | C、48 | D、144 |
 14、如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为
14、如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为 如图,在?ABCD中,E为CD的中点,AE交BD于点F,则△EFD和△AFB的面积比为
如图,在?ABCD中,E为CD的中点,AE交BD于点F,则△EFD和△AFB的面积比为 如图,在?ABCD中,BD为对角线,EF垂直平分BD分别交AD、BC的于点E、F,交BD于点O.
如图,在?ABCD中,BD为对角线,EF垂直平分BD分别交AD、BC的于点E、F,交BD于点O.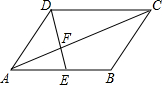 如图,在?ABCD中,E为AB的中点,DE交AC于F,△AEF∽
如图,在?ABCD中,E为AB的中点,DE交AC于F,△AEF∽