题目内容
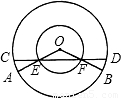
 54、如图,已知以O为圆心的两个同心圆中,大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于A、B,求证:AC=BD.
54、如图,已知以O为圆心的两个同心圆中,大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于A、B,求证:AC=BD.分析:连接OC、OD,则△OCD和△OEF都是等腰三角形,有∠OCD=∠ODC,∠OEF=∠OFE,
由三角形的外角等于与它不相邻的两个内角和,得∠AOC=∠BOD,再由在同圆中相等的圆心角对的弧相等得,AC=BD.
由三角形的外角等于与它不相邻的两个内角和,得∠AOC=∠BOD,再由在同圆中相等的圆心角对的弧相等得,AC=BD.
解答:证明:连接OC、OD,
∵OC=OD,OE=OF,
∴∠OCD=∠ODC,∠OEF=∠OFE,
∠OEF=∠C+∠COA=∠D+∠BOD=∠OFE,
∴∠AOC=∠BOD,
∴AC=BD.
∵OC=OD,OE=OF,
∴∠OCD=∠ODC,∠OEF=∠OFE,
∠OEF=∠C+∠COA=∠D+∠BOD=∠OFE,
∴∠AOC=∠BOD,
∴AC=BD.
点评:本题利用了等边对等角,三角形的外角与内角的关系和在同圆中相等的圆心角对的弧相等求解.

练习册系列答案
相关题目
 如图,已知以AB为直径,O为圆心的半圆与直线MN相切于点C,∠A=28°.
如图,已知以AB为直径,O为圆心的半圆与直线MN相切于点C,∠A=28°. 如图,已知以AB为直径的圆与x轴交于A、B两点,与y轴交于C、D两点,A、C 两点的坐标分别为A(-1,0)、C(0,3),直线DE交x轴交于点E(-
如图,已知以AB为直径的圆与x轴交于A、B两点,与y轴交于C、D两点,A、C 两点的坐标分别为A(-1,0)、C(0,3),直线DE交x轴交于点E(- 如图,已知以O为圆心的两个同心圆中,大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于A、B,求证:AC=BD.
如图,已知以O为圆心的两个同心圆中,大圆的弦CD交小圆于E、F,OE、OF的延长线交大圆于A、B,求证:AC=BD.