题目内容
3.在四边形ABCD中,O是对角线交点,不能判定四边形ABCD是矩形的是( )| A. | ∠ABC=∠BCD=∠CDA=90° | B. | AD=BC,AD∥BC,AC⊥BD | ||
| C. | OA=OB=OC=OD | D. | AB=CD,AD=BC,∠BAD=90° |
分析 矩形的判定定理有:
(1)有一个角是直角的平行四边形是矩形.
(2)有三个角是直角的四边形是矩形.
(3)对角线互相平分且相等的四边形是矩形.据此判断.
解答 解:A、三个角是直角的四边形是为矩形,故A正确.
B、∵AD=BC,AD∥BC,∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD是菱形,故错误;
C、矩形的对角线平分且相等,故C正确.
D、因为AB=CD,AD=BC,故四边形ABCD是平行四边形,又因为∠BAD=90°,根据矩形的判定(有一个角是直角的平行四边形是矩形),故D正确.
故选B.
点评 本题考查的是矩形的判定定理,但考生应注意的是由矩形的判定引申出来的各图形的判定.难度一般.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
8.直线y=2x-3与直线y=kx+1平行,则k等于( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
 已知:如图,四边形ABCD中,∠A=∠C,AB∥CD.求证:AD∥BC.
已知:如图,四边形ABCD中,∠A=∠C,AB∥CD.求证:AD∥BC.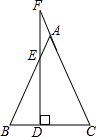 如图所示,在△ABC中,AB=AC,点D是底边BC上的一个动点,过点D作BC的垂线分别交一腰和另一腰的延长线于点E、F.
如图所示,在△ABC中,AB=AC,点D是底边BC上的一个动点,过点D作BC的垂线分别交一腰和另一腰的延长线于点E、F.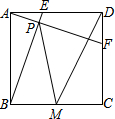 如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为$\sqrt{10}$.
如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为$\sqrt{10}$.