题目内容
6.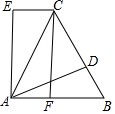 如图,△ABC是等边三角形,D是BC上一点,△ABD经旋转后到达△ACE的位置.
如图,△ABC是等边三角形,D是BC上一点,△ABD经旋转后到达△ACE的位置.(1)旋转中心是点A;∠EAD=60°;
(2)若点F是AB上的一点且AF=BD,连接CF,求证:四边形AFCE是平行四边形.
分析 (1)根据△ABD经旋转后到达△ACE的位置,可得旋转中心,再根据旋转的性质以及等边三角形的性质,即可得出∠EAD的度数;
(2)根据一组对边平行且相等的四边形是平行四边形进行证明即可.
解答  解:(1)由旋转可得,旋转中心是点A,∠BAD=∠CAE,
解:(1)由旋转可得,旋转中心是点A,∠BAD=∠CAE,
∵△ABC是等边三角形,
∴∠BAD+∠CAD=∠CAE+∠CAD=60°,
∴∠EAD=60°;
故答案为:A,60;
(2)∵∠CAB=∠B=∠ACE=60°,
∴AF∥CE,
又∵AF=BD=EC,
∴四边形AFCE是平行四边形.
点评 本题主要考查了旋转的性质以及平行四边形的判定,解决问题的关键是运用旋转前、后的图形全等进行解题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
1.下列运算正确的是( )
| A. | -a+b+c+d=-(a-b)-(-c-d) | B. | x-(y-z)=x-y-z | ||
| C. | x+2y-2z=x-2(z+y) | D. | -(x-y+z)=-x-y-z |
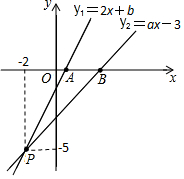 如图,已知函数y1=2x+b和y2=ax-3的图象交于点P (-2,-5),这两个函数的图象与x轴分别交于点A、B.
如图,已知函数y1=2x+b和y2=ax-3的图象交于点P (-2,-5),这两个函数的图象与x轴分别交于点A、B. 如图,C,D是线段AB上两点,D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长等于多少?
如图,C,D是线段AB上两点,D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长等于多少?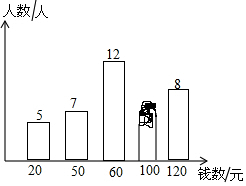 小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.
小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.