题目内容
如图,点![]() 是以
是以![]() 为直径的⊙
为直径的⊙![]() 上的一点,
上的一点,![]() 与过点
与过点![]() 的切线互相垂
的切线互相垂![]() 直,垂足为点
直,垂足为点![]()
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,求⊙
,求⊙![]() 的半径长.
的半径长.
 (1)证明:连接
(1)证明:连接![]()
![]()
![]()
![]() ∴∠
∴∠![]() =∠
=∠![]()
![]()
![]() 切⊙
切⊙![]() 于
于![]() ∴
∴![]()
![]()
![]()
∴![]()
又![]()
![]()
![]()
∴![]() ∴
∴![]() +
+![]()
![]()
![]() ∥
∥![]()
![]()
![]() =∠
=∠![]()
![]()
![]()
![]() 平分
平分![]()
(2)解法一:如图,过点![]() 作
作![]()
![]() 于
于![]()
在![]() △
△![]() 中,
中,![]() =
=![]()
![]() =
=![]() ∵
∵![]() ∴
∴![]() =
=![]()
![]() =
=![]()
![]()
![]() ,
,![]()
![]()
![]() △
△![]() ∽△
∽△![]()
![]()
![]() 即
即
![]()
![]() =
=![]() 即⊙
即⊙![]() 的半径为
的半径为![]() .解法二:如图,连接
.解法二:如图,连接![]()
![]() 在
在![]() △
△![]() 中,
中,![]() =
=![]()
![]() =
=![]()

![]()
![]() 是⊙
是⊙![]() 直径,
直径,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() △
△![]() ∽△
∽△![]()
![]()
![]() 即
即![]()
![]()
![]() =
=![]()
![]()
![]() =
=![]()
即⊙![]() 的半径为
的半径为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, ,
, ,点
,点 是以
是以 为直径的半圆
为直径的半圆 上一动点,
上一动点, 交直线
交直线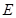 ,设
,设 .
. 时,求
时,求 的长;
的长; 时,求线段
时,求线段 的长;
的长; 的延长线上,则
的延长线上,则 的取值范围是_______.(直接写出答案)
的取值范围是_______.(直接写出答案)
 ,
, ,
, ,点
,点 是以
是以 为直径的半圆
为直径的半圆 上一动点,
上一动点,  交直线
交直线 ,设
,设 .
. 时,求
时,求 的长;
的长; 时,求线段
时,求线段 的长;
的长; 的延长线上,则
的延长线上,则 的取值范围是_______.(直接写出答案)
的取值范围是_______.(直接写出答案)
 ,
, ,
, ,点
,点 是以
是以 为直径的半圆
为直径的半圆 上一动点,
上一动点,  交直线
交直线 于点
于点 ,设
,设 .
. 时,求弧BD的长;
时,求弧BD的长; 时,求线段
时,求线段 的长;
的长; 在线段
在线段 的延长线上,则
的延长线上,则 的取值范围( )
的取值范围( )