Question

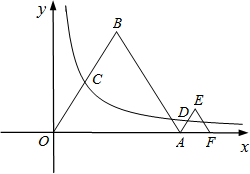（2012•江岸区模拟）等边△OAB和△AEF的一边都在x轴上，双曲线y=

k

x

（k＞0）经过边OB的中点C和AE的中点D．已知：OA=2，则△AEF的边长为

-4+2

5

．

Answer 1

分析：过C作CG⊥x轴，过D作DH⊥x轴，由△OAB为等边三角形，OA=2，C为OB的中点，得到∠BOA=60°，OC=1，在直角三角形OCG中，利用三角函数定义求出OG与CG的长，确定出C的坐标，代入反比例解析式中求出k的值，确定出反比例解析式，设等边△AEF的边长为a，由△AEF为等边三角形，AE=AF=EF=a，C为OB的中点，得到∠EAF=60°，表示出AD，同理表示出AH与DH的长，由OA+AH表示出OH的长，进而表示出D的坐标，代入反比例解析式中求出a的值，即为三角形AEF的边长．

解答：解：过C作CG⊥x轴，过D作DH⊥x轴，
∵△OAB为等边三角形，OA=2，C为OB的中点，
∴∠BOA=60°，OC=1，
在Rt△OCG中，sin∠BOA=

CG

OC

，cos∠BOA=

OG

OC

，
∴CG=OC•sin∠BOA=

3

2

，OG=OC•cos∠BOA=

1

2

，
∴C（

1

2

，

3

2

），
将C坐标代入反比例解析式中得：k=

3

4

，
∴反比例解析式为y=

3

4x

，
设等边△AEF的边长为a，
∵△AEF为等边三角形，AE=AF=EF=a，C为OB的中点，
∴∠EAF=60°，AD=

1

2

a，
同理得到AH=

1

4

a，DH=

3

4

a，
∴OH=OA+AH=2+

1

4

a，
∴D（2+

1

4

a，

3

4

a），
代入反比例函数解析式得：

3

4

a（2+

1

4

a）=

3

4

，即a（2+

1

4

a）=1，
整理得：8a+a²=4，即a²+8a-4=0，
解得：a=

-8±4 5

2

=-4±2

5

，
而a=-4-2

5

不合题意，舍去，故a=-4+2

5

，
则等边△AEF的边长为-4+2

5

．
故答案为：-4+2

5

．

点评：此题考查了反比例函数综合题，涉及的知识有：坐标与图形性质，三角函数定义，等边三角形的性质，以及待定系数法求反比例解析式，熟练掌握待定系数法是解本题的关键．