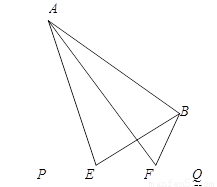
题目内容
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).(参考数据:![]() ≈1.73,
≈1.73,
sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
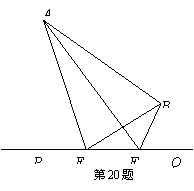 | |||
 | |||
解: 1)过点B作BD∥AE,交AC于点D。
因为 36×0.5=18(海里),∠ADB=60°,∠DBC=30°,所以∠ACB=30°。
又∠CAB=30°,所以BC=AB,即BC=AB=18>16 ,所以点B在暗礁区域外。(2)过点C作CH⊥AB,垂足为H。
在Rt△CHB中,∠BCH=30°,令BH=x(海里),则 CH=√3X(海里)。
在Rt△ACH中,∠CAH=30°,所以 AH=3X(海里)。
因为 AH=AB+BH,所以 3X=18+X,解得X=9 ,所以 CH=9√3海里<16海里。
所以船继续向东航行有触礁的危险。

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
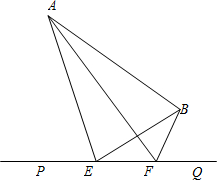 如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.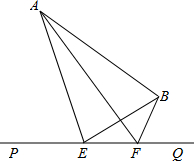 如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=70°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=70°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=

 如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.