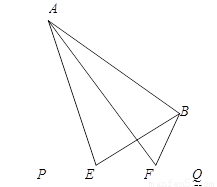
题目内容
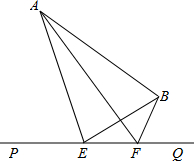 如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=70°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=(4
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=70°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=(4| 3 |
(1)判断线段AB与AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离.(sin70°≈
| 12 |
| 13 |
| 5 |
| 13 |
分析:(1)根据SAS即可证明△AEF≌△ABF,得到AB=AE;
(2)作AH⊥PQ,垂足为H.设AE=x,在直角△AHF,直角△AEP中,利用三角函数表示出HE与HF,从而可得到关于x的方程,解方程即可得解.
(2)作AH⊥PQ,垂足为H.设AE=x,在直角△AHF,直角△AEP中,利用三角函数表示出HE与HF,从而可得到关于x的方程,解方程即可得解.
解答:解:(1)相等.
∵∠BEQ=30°,∠BFQ=60°,
∴∠EBF=∠BEQ=30°,
∴EF=BF,
又∵∠AFP=60°,
∴∠BFA=60°.
在△AEF与△ABF中,
∵
,
∴△AEF≌△ABF(SAS),
∴AB=AE;
(2)过点A作AH⊥PQ,垂足为H.
设AE=xkm,
则AH=xsin70°km,HE=xcos70°km,
∴HF=HE+EF=xcos70°+4
-5(km),
Rt△AHF中,AH=HF•tan60°,
∴xsin70°=(xcos70°+4
-5)•tan60°,
即:
x=(
x+4
-5)×
,
解得:x≈13,
即AB=AE=13km.
答:两个岛屿A与B之间的距离约为13km.
∵∠BEQ=30°,∠BFQ=60°,
∴∠EBF=∠BEQ=30°,
∴EF=BF,
又∵∠AFP=60°,
∴∠BFA=60°.
在△AEF与△ABF中,
∵
|

∴△AEF≌△ABF(SAS),
∴AB=AE;
(2)过点A作AH⊥PQ,垂足为H.
设AE=xkm,
则AH=xsin70°km,HE=xcos70°km,
∴HF=HE+EF=xcos70°+4
| 3 |
Rt△AHF中,AH=HF•tan60°,
∴xsin70°=(xcos70°+4
| 3 |
即:
| 12 |
| 13 |
| 5 |
| 13 |
| 3 |
| 3 |
解得:x≈13,
即AB=AE=13km.
答:两个岛屿A与B之间的距离约为13km.
点评:此题考查了方向角问题.注意能运用了三角函数,把求线段的问题转化为方程求解的问题是解此题的关键,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
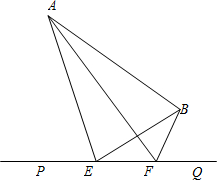 如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.

 如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.