题目内容
5.解方程:(1)3x2-5x-2=0
(2)x2-6x=5
(3)2x2-6x-1=0
(4)3x(x+2)=5(x+2)
分析 (1)根据因式分解法可以解答此方程;
(2)根据配方法可以解答此方程;
(3)根据公式法可以解答此方程;
(4)先移项,然后根据提公因式法可以解答此方程.
解答 解:(1)3x2-5x-2=0
(3x+1)(x-2)=0
∴3x+1=0或x-2=0,
解得,${x}_{1}=-\frac{1}{3},{x}_{2}=2$;
(2)x2-6x=5
(x-3)2=14,
x-3=$±\sqrt{14}$,
∴${x}_{1}=3-\sqrt{14},{x}_{2}=3+\sqrt{14}$;
(3)2x2-6x-1=0
a=2,b=-6,c=-1
∵△=(-6)2-4×2×(-1)=44>0,
∴x=$\frac{6±\sqrt{44}}{2×2}=\frac{3±\sqrt{11}}{2}$,
∴${x}_{1}=\frac{3-\sqrt{11}}{2},{x}_{2}=\frac{3+\sqrt{11}}{2}$;
(4)3x(x+2)=5(x+2)
3x(x+2)-5(x+2)=0
(x+2)(3x-5)=0
∴x+2=0或3x-5=0,
解得,${x}_{1}=-2,{x}_{2}=\frac{5}{3}$.
点评 本题考查解一元二次方程-因式分解法(配方法、公式法),解题的关键是根据方程的特点选取合适的方法进行解答.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
 如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.
如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.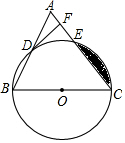 如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D,E,DF⊥AC于点F.
如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D,E,DF⊥AC于点F. 如图,点C为直线l上一点,A、B为直线l外两点,过A、B两点分别作直线l的垂线,垂足为点D、E,连接BC、AB,且AB交直线l于点F,若AC=BC,AD=CE,求证:
如图,点C为直线l上一点,A、B为直线l外两点,过A、B两点分别作直线l的垂线,垂足为点D、E,连接BC、AB,且AB交直线l于点F,若AC=BC,AD=CE,求证: