题目内容
18.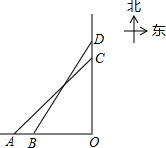 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
分析 设B处距离码头Oxkm,分别在Rt△CAO和Rt△DBO中,根据三角函数求得CO和DO,再利用DC=DO-CO,得出x的值即可.
解答 解:设B处距离码头Oxkm,
在Rt△CAO中,∠CAO=45°,
∵tan∠CAO=$\frac{CO}{AO}$,
∴CO=AO•tan∠CAO=(45×0.1+x)•tan45°=4.5+x,
在Rt△DBO中,∠DBO=58°,
∵tan∠DBO=$\frac{DO}{BO}$,
∴DO=BO•tan∠DBO=x•tan58°,
∵DC=DO-CO,
∴36×0.1=x•tan58°-(4.5+x),
∴x=$\frac{36×0.1+4.5}{tan58°-1}$≈$\frac{36×0.1+4.5}{1.60-1}$=13.5.
因此,B处距离码头O大约13.5km.
点评 本题考查了解直角三角形的应用,熟练掌握三角形中的边角关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑦个图形中小圆圈的个数为( )


| A. | 21 | B. | 24 | C. | 27 | D. | 30 |
10.在正方形、矩形、菱形、平行四边形、等腰梯形中,其中中心对称图形的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
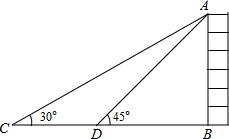 如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)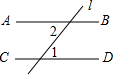 如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为50°.
如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为50°.
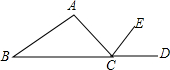 如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是60度.
如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是60度.