Question

【题目】如图，在△ABC中，点E，F分别为BC上的点，EF＝，∠BAC＝135°，∠EAF＝90°，tan∠AEF＝1.

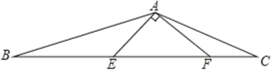
（1）若1＜BE＜2，求CF的取值范围；

（2）若AB＝，求△ACF的面积．

Answer 1

【答案】（1）1＞CF＞；（2）S△ACF＝.

【解析】

（1）由已知tan∠AEF＝1，∠EAF＝90°易证得△AEF为等腰直角三角形，也易证得△BAE∽△ACF，利用相似三角形对应边成比例可得，根据已知1＜BE＜2，可求得结论；

（2）作AH⊥BC于H，先求得等腰直角三角形△AEF的高，利用勾股定理求得BH的长，继而求得BE的长，利用（1）的结论求得CF，从而求得△ACF的面积．

（1）∵∠BAC＝135°，∠EAF＝90°，

∴∠BAE+∠CAF＝45°，

∵tan∠AEF＝1，

∴∠AEF＝∠AFE＝45°，△AEF为等腰直角三角形，

∴∠B+∠BAE＝45°，∠C+∠FAC＝45°，

∴∠B＝∠CAF，∠C＝∠BAE，

∴△BAE∽△ACF

∴；

∵EF＝，△AEF为等腰直角三角形，

∴AE＝AF＝1

∴．

∵1＜BE＜2，

∴1＞CF＞．

（2）过点A作AH⊥BC于H，

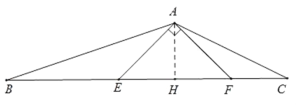
∵EF＝，△AEF为等腰直角三角形，

∴AH＝EH＝HF＝，

又∵AB＝，

∴，

∴BE＝BH﹣EH＝，

由（1）得∴，

S△ACF＝×CFAH＝.