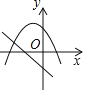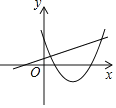题目内容
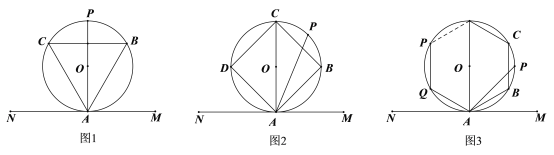
【题目】如图1,![]() 是⊙O内接等边三角形,直线MN与⊙O相切于A点,P是弧BC的中点,则
是⊙O内接等边三角形,直线MN与⊙O相切于A点,P是弧BC的中点,则![]() .
.
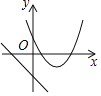
(1)如图2,正方形ABCD是⊙O内接正方形,直线MN与⊙O相切于A点,P是弧BC的中点,则![]() ________;
________;
(2)如图3,若正n边形ABC……PQ是⊙O内接正n边形,直线MN与⊙O相切于A点,P是弧BC的中点,若![]() 的度数小于
的度数小于![]() ,则n的最小值是_______.
,则n的最小值是_______.
【答案】(1)![]() ;(2)10
;(2)10
【解析】
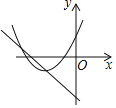
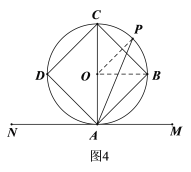
(1)连接OP、OB,如图4,由题意可得∠COB=90°,进而可得∠COP的度数,再根据圆周角定理可得∠CAP的度数,然后用90°减去∠CAP即为所求;
(2)如图5,连接OC、OP、OB,则∠AOB=∠BOC=![]() ,根据三角形的内角和定理和圆周角定理可用含n的代数式求出∠BAM和∠PAB,即得∠PAM,然后根据题意可得关于n的不等式,解不等式即可求得n的范围,进一步即可求出结果.
,根据三角形的内角和定理和圆周角定理可用含n的代数式求出∠BAM和∠PAB,即得∠PAM,然后根据题意可得关于n的不等式,解不等式即可求得n的范围,进一步即可求出结果.
解:(1)连接OP、OB,如图4,∵正方形ABCD是⊙O内接正方形,∴∠COB=90°,
∵P是弧BC的中点,∴∠COP=45°,∴∠CAP=![]() =22.5°,
=22.5°,
∴![]() ∠CAM-∠CAP=90°-22.5°=67.5°;
∠CAM-∠CAP=90°-22.5°=67.5°;
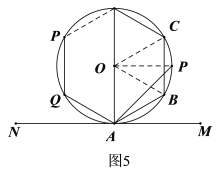
(2)如图5,连接OC、OP、OB,则OA=OB,∠AOB=∠BOC=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵P是弧BC的中点,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,
由于n为整数,所以n的最小值为10.
故答案为:(1)![]() ;(2)10.
;(2)10.

练习册系列答案
相关题目