题目内容
如图所示，已知梯形ABCD，AD∥BC，E为CD的中点，若用S1、S2、S3分别表示△ADE、△EBC、△ABE的面积，则S1、S2、S3的关系是
- A.S1+S2＞S3
- B.S1+S2=S3
- C.S1+S2＜S3
- D.以上都不对
B
分析：延长AE，交BC延长线于点F，则可得到△ADE≌△FCE，则AE=EF，从而得到△AEB与△BFE是等底同高的两个三角形，即它们的面积相等，则三者的关系不难得出．
解答：
解：如图，延长AE，交BC延长线于点F，
∵AD∥BC，E为CD的中点，
∴△ADE≌△FCE，点E是AF的中点，有AE=EF，
∴△AEB与△BFE是等底同高的两个三角形，即它们的面积相等，
∴S△BFE=S1+S2=S3故选B．
点评：本题考查梯形，三角形的相关知识．解决此类题要懂得用梯形的常用辅助线，把梯形分割为几个三角形，从而由三角形的性质来求解．
分析：延长AE，交BC延长线于点F，则可得到△ADE≌△FCE，则AE=EF，从而得到△AEB与△BFE是等底同高的两个三角形，即它们的面积相等，则三者的关系不难得出．
解答：
解：如图，延长AE，交BC延长线于点F，∵AD∥BC，E为CD的中点，
∴△ADE≌△FCE，点E是AF的中点，有AE=EF，
∴△AEB与△BFE是等底同高的两个三角形，即它们的面积相等，
∴S△BFE=S1+S2=S3故选B．
点评：本题考查梯形，三角形的相关知识．解决此类题要懂得用梯形的常用辅助线，把梯形分割为几个三角形，从而由三角形的性质来求解．
练习册系列答案
一线名师提优试卷系列答案
相关题目
19、如图所示，已知梯形ABCD，AD∥BC，E为CD的中点，若用S1、S2、S3分别表示△ADE、△EBC、△ABE的面积，则S1、S2、S3的关系是（ ）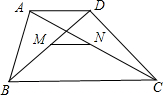
如图所示，已知梯形ABCD中，AD∥BC，且AD＜BC，N、M分别为AC、BD的中点，
32、如图所示，已知梯形ABCD中，AB∥CD，AD=BC，中位线EF=15cm，∠DAB=60°，且AC平分∠DAB，则梯形的周长是
10、如图所示，已知梯形纸片ABCD中，∠B=60°，将纸片沿着对角线AC折叠，折叠后点D刚好落在AB边上的点E处．小明认为：如果E是AB的中点，则梯形ABCD是等腰梯形；小亮认为：如果梯形ABCD是等腰梯形，则E是AB的中点．对于他们两人的说法，你认为（ ）
如图所示，已知梯形ABCD中，AD∥BC，请你利用中心对称的性质，把梯形ABCD转化成与原梯形面积相等的三角形，并简要说明变换理由．