题目内容
 已知如图,OP是∠AOB的平分线,M为OP上一点,E,F是OA上任意两点,C,D是OB上任意两点,且EF=CD,则△FEM与△CDM的面积大小关系为:S△FEM
已知如图,OP是∠AOB的平分线,M为OP上一点,E,F是OA上任意两点,C,D是OB上任意两点,且EF=CD,则△FEM与△CDM的面积大小关系为:S△FEM分析:利用角的平分线上的点到角的两边的距离相等可知这两个三角形的高相等,由已知条件又知底也相等,所以面积相等.
解答:解:S△EFM=S△CDM.
理由:作MN⊥OA于N,MH⊥OB于H,

∵OP平分∠AOB,MN⊥OA,MH⊥OB,
∴MN=MH,
∴S△EFM=
•EF•MN,S△CDM=
CD•MH.
又∵EF=CD,
∴S△EFM=S△CDM.
故填=.
理由:作MN⊥OA于N,MH⊥OB于H,

∵OP平分∠AOB,MN⊥OA,MH⊥OB,
∴MN=MH,
∴S△EFM=
| 1 |
| 2 |
| 1 |
| 2 |
又∵EF=CD,
∴S△EFM=S△CDM.
故填=.
点评:本题主要考查角平分线上点到角的两边的距离相等的性质和三角形面积求法.正确作出辅助线是解答本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
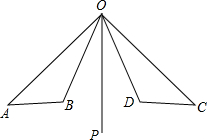 已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD.求证:AB=CD.
已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD.求证:AB=CD.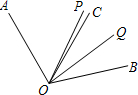 已知如图,∠AOC=60°,∠BOC=50°,OP平分∠AOB,OQ平分∠BOC.
已知如图,∠AOC=60°,∠BOC=50°,OP平分∠AOB,OQ平分∠BOC. 已知如图,OP是∠AOB的平分线,M为OP上一点,E,F是OA上任意两点,C,D是OB上任意两点,且EF=CD,则△FEM与△CDM的面积大小关系为:S△FEM________S△CDM.(请填“>”、“<”或“=”)
已知如图,OP是∠AOB的平分线,M为OP上一点,E,F是OA上任意两点,C,D是OB上任意两点,且EF=CD,则△FEM与△CDM的面积大小关系为:S△FEM________S△CDM.(请填“>”、“<”或“=”)