题目内容
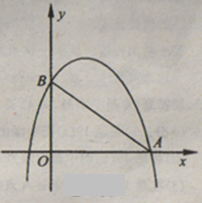
如图,已知二次函数y= -x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.
1.求此二次函数关系式和点B的坐标;
2.在x轴的正半轴上是否存在点P,使得△PAB是以AB为底的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【解析】
3.把点A的坐标代入二次函数,求出b的值,确定二次函数关系式,把x=0代入二次函数求出点B的坐标.
4.分情况讨论,①当BP=AP时,②当AB=AP时,分别求出即可得出答案.
-x2+bx+3的图象与x轴的一个交点为A(4,0),
∴0=-42+4b+3,
解得b=![]() ,
,
∴此二次函数关系式为:y= -x2+![]() x+3,
x+3,
点B的坐标为B(0,3).
4.在x轴的正半轴上是否存在点P(![]() ,0),使得△PAB是以AB为底的等腰三角形.理由如下:
,0),使得△PAB是以AB为底的等腰三角形.理由如下:
设点P(x,0),x>0,则根据下图和已知条件可得
x2+ 32=(4- x)2,
解得x=![]() ,
,
∴点P的坐标为P( ,0).
,0).
即,在x轴的正半轴上是否存在点P(![]() ,0),使得△PAB是以AB为底的等腰三角形.
,0),使得△PAB是以AB为底的等腰三角形.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
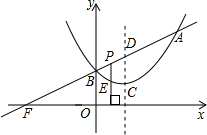 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.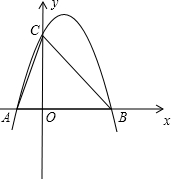
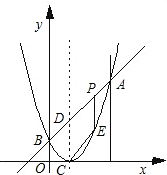 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.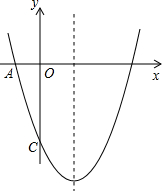 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).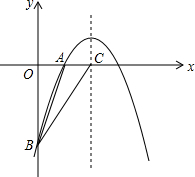 (2012•衡水一模)如图,已知二次函数
(2012•衡水一模)如图,已知二次函数