题目内容

A（-2，y₁）、B（-1，y₂）两点在反比例函数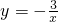 $数学公式$ 图象上，则y₁________y₂（填“＜”、“＞”、“=”）．

＜
分析：先根据反比例函数的解析式判断出函数图象所在的象限及其增减性，再根据A、B两点的横坐标判断出两点所在的象限，故可得出结论．
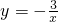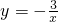解答：∵反比例函数 $\text{[math]}$ 中k=-3＜0，
∴该函数的图象的两个分支在二、四象限，在每一象限内y随x的增大而增大，
∵-2＜0，-1＜0，
∴A、B两点在第二象限，
∵-2＜-1，
∴y₁＜y₂．
故答案为：＜．
点评：本题考查的是反比例函数图象上点的坐标特点，即反比例函数图象上各点的坐标一定适合此函数的解析式．

练习册系列答案

昕金立文化中考一本全系列答案

模拟试卷汇编优化系列答案

学期总复习期末复习寒假作业系列答案

赢在课堂中考先锋总复习卷系列答案

中考风向标全国中考试题精析系列答案

宏翔教育中考金牌中考总复习系列答案

赢在中考3年中考2年模拟系列答案

宏翔文化中考亮剑系列答案

5年中考江苏13大市中考真题历年回顾精选28套卷系列答案

薪火文化假期百分百系列答案

相关题目

已知二次函数y=-

，设自变量的值分别为x₁，x₂，x₃，且-3＜x₁＜x₂＜x₃，则对应的函数值y₁，y₂，y₃的大小关系是（　　）

A、y₁＞y₂＞y₃

B、y₁＜y₂＜y₃

C、y₂＞y₃＞y₁

D、y₂＜y₃＜y₁

先阅读下面的材料，再解答下面的各题．
在平面直角坐标系中，有AB两点，A（x₁，y₁）、B（x₂，y₂）两点间的距离用|AB|表示，则有|AB|=

(x1-x2)2+(y1-y2)2

，下面我们来证明这个公式：证明：如图1，过A点作X轴的垂线，垂足为C，则C点的横坐标为x₁，过B点作X轴的垂线，垂足为D，则D点的横坐标为x₂，过A点作BD的垂线，垂足为E，则E点的横坐标为x₂，纵坐标为y₁．∴|AE|=|CD|=|x₁-x₂|
|BE|=|BD|-|DE|=|y₂-y₁|=||y₁-y₂|
在Rt△AEB中，由勾股定理得|AB|²=|AE|²+|BE|²=|x₁-x₂|²+|y₁-y₂|²
∴|AB|=

(x1-x2)2+(y1-y2)2

（因为|AB|表示线段长，为非负数）
注：当A、B在其它象限时，同理可证上述公式成立．
（1）在平面直角坐标系中有P（4，6）、Q（2，-3）两点，求|PQ|．
（2）如图2，直线L₁与L₂相交于点C（4，6），L₁、L₂与X轴分别交于B、A两点，其坐标B（8，0）、A（1，0），直线L₃平行于X轴，与L₁、L₂分别交于E、D两点，且|DE|=

，求线段|DA|的长．

已知：关于x的一元二次方程x²+（n-2m）x+m²-mn=0①
（1）求证：方程①有两个实数根；
（2）若m-n-1=0，求证：方程①有一个实数根为1；
（3）在（2）的条件下，设方程①的另一个根为a．当x=2时，关于m的函数y₁=nx+am与y₂=x²+a（n-2m）x+m²-mn的图象交于点A、B（点A在点B的左侧），平行于y轴的直线L与y₁、y₂的图象分别交于点C、D．当L沿AB由点A平移到点B时，求线段CD的最大值．

一次函数y=-kx+4与反比例函数y=

的图象上有两个不同的交点，点（-

，y₁），（-1，y₂），（

，y₃）是函数y=

的图象上的三点，则y₁，y₂，y₃的大小关系为

如图所示，在等腰三角形ABC中，∠B=90°，AB=BC=4米，点P以1米/分的速度从A点出发移动到

B点，同时点Q以2米/分的速度从点B移动到C点（当一个点到达后全部停止移动）．
（1）设经过x分钟后，△PCB的面积为y₁，△QAB的面积为y₂，求出y₁，y₂关于x的函数关系式；
（2）同时移动多少分钟，这两个三角形的面积相等？
（3）移到时间在什么范围内时，①△PCB的面积大于△QAB的面积？②△PCB的面积小于△QAB的面积？