题目内容
当 时,求
时,求 的值.
的值.
解:原式= -
-
= -
- ,
,
∵a=2- <1,
<1,
∴原式= -
-
=-a+1
=-(2- )+1
)+1
= -1.
-1.
分析:先根据二次根式的性质化简原式得到原式= -
- =
= -
- ,再根据a=2-
,再根据a=2- <1去绝对值得到原式=-a+1,然后把a的值代入计算即可.
<1去绝对值得到原式=-a+1,然后把a的值代入计算即可.
点评:本题考查了二次根式的化简求值:先把各二次根式化为最简二次根式(或整式),再合并同类二次根式,然后把满足条件的字母的值代入计算.
 -
-
=
 -
- ,
,∵a=2-
 <1,
<1,∴原式=
 -
-
=-a+1
=-(2-
 )+1
)+1=
 -1.
-1.分析:先根据二次根式的性质化简原式得到原式=
 -
- =
= -
- ,再根据a=2-
,再根据a=2- <1去绝对值得到原式=-a+1,然后把a的值代入计算即可.
<1去绝对值得到原式=-a+1,然后把a的值代入计算即可.点评:本题考查了二次根式的化简求值:先把各二次根式化为最简二次根式(或整式),再合并同类二次根式,然后把满足条件的字母的值代入计算.

练习册系列答案
相关题目
 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
. 的取值范围;
的取值范围; 时,求
时,求 的平分线
的平分线 分别与
分别与 、
、 交于点
交于点 、
、 .
.
 ;
; 时,求
时,求 的值.
的值. .
. 时,求
时,求 的值;
的值; 时,求
时,求 的值.
的值. (
( 为常数,
为常数, )上任一点,将抛物线绕顶点
)上任一点,将抛物线绕顶点 逆时针旋转
逆时针旋转 后得到的新图象与
后得到的新图象与 轴交于
轴交于 、
、 两点(点
两点(点 为点
为点 旋转后的对应点.
旋转后的对应点.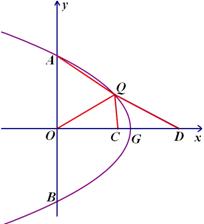
 ,点
,点 ,用含
,用含 的代数式表示
的代数式表示 ;
; 在
在 轴的正半轴上,点
轴的正半轴上,点 为
为 的中点,
的中点, 平分
平分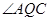 ,
, ,当
,当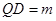 时,求
时,求