题目内容
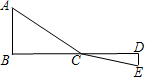 阅读材料:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为
阅读材料:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为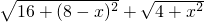 .然后利用几何知识可知:当x=
.然后利用几何知识可知:当x= 时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式
时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式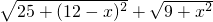 的最小值为________.
的最小值为________.
4
分析:根据已知图象,重新构造直角三角形,利用三角形相似得出CD的长,进而利用勾股定理得出最短路径问题.
解答: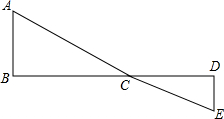 解:如图所示:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,
解:如图所示:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,
若AB=5,DE=3,BD=12,
当A,C,E,在一条直线上,AE最短,
∵AB⊥BD,ED⊥BD,
∴AB∥DE,
∴△ABC∽EDC,
∴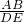 =
=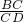 ,
,
∴ =
=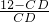 ,
,
解得:DC= .
.
即当x= 时,代数式
时,代数式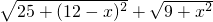 的最小值,
的最小值,
此时为: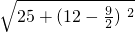 +
+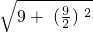 =
= +
+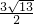 =4
=4 .
.
故答案为:4 .
.
点评:此题主要考查了求最短路线问题,利用了数形结合的思想,求形如的式子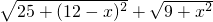 的最小值,可通过构造直角三角形,利用勾股定理求解.
的最小值,可通过构造直角三角形,利用勾股定理求解.

分析:根据已知图象,重新构造直角三角形,利用三角形相似得出CD的长,进而利用勾股定理得出最短路径问题.
解答:
 解:如图所示:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,
解:如图所示:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=5,DE=3,BD=12,
当A,C,E,在一条直线上,AE最短,
∵AB⊥BD,ED⊥BD,
∴AB∥DE,
∴△ABC∽EDC,
∴
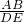 =
=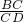 ,
,∴
 =
=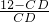 ,
,解得:DC=
 .
.即当x=
 时,代数式
时,代数式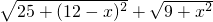 的最小值,
的最小值,此时为:
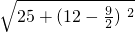 +
+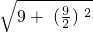 =
= +
+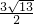 =4
=4 .
.故答案为:4
 .
.点评:此题主要考查了求最短路线问题,利用了数形结合的思想,求形如的式子
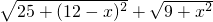 的最小值,可通过构造直角三角形,利用勾股定理求解.
的最小值,可通过构造直角三角形,利用勾股定理求解. 
练习册系列答案
相关题目
 (2012•金牛区二模)阅读材料:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为
(2012•金牛区二模)阅读材料:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为 .然后利用几何知识可知:当x=
.然后利用几何知识可知:当x= 时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式
时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式 的最小值为 .
的最小值为 .
 .然后利用几何知识可知:当x=
.然后利用几何知识可知:当x= 时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式
时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式 的最小值为 .
的最小值为 .
 .然后利用几何知识可知:当x=
.然后利用几何知识可知:当x= 时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式
时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式 的最小值为 .
的最小值为 .
 .然后利用几何知识可知:当x=
.然后利用几何知识可知:当x= 时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式
时,AC+CE的最小值为10.根据以上阅读材料,可构图求出代数式 的最小值为 .
的最小值为 .