题目内容
10.某农户2015年承包荒山若干亩,投资7800元改造后,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=1.3元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
(3)在上面的问题(2)的条件下,该农户加强果园管理,力争到明年纯收入达到15000元,而且该农户采用了(2)中较好的出售方式出售,那么纯收入增长率是多少(纯收入=总收入-总支出)?
分析 (1)市场出售收入=水果的总收入-额外支出.而水果直接在果园的出售收入为:18000b.
(2)根据(1)中得到的代数式,将a=1.3,b=1.1,代入代数式计算即可.
(3)根据(2)的数据,首先确定今年的最高收入,然后计算增长率即可.
解答 解:(1)将此水果拉到市场出售收入为:
18000a-(25×8+100)×$\frac{18000}{1000}$=(18000a-5400)元.
将此水果直接在果园出售收入为:18000b.
(2)当a=1.3,b=1.1,市场出售收入为:18000a-5400=18000×1.3-5400=18000元.
果园出售收入为:18000b=18000×1.1=19800元.
显然,18000<19800,宜在果园出售.
(3)今年的最高纯收入为:19800-7800=12000元,
增长率=$\frac{15000-12000}{12000}$×100%=25%.
点评 本题考查了根据实际问题列代数式,把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.解题的关键是读懂题意,正确表达.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
2.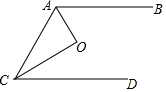 如图,已知AB∥CD,O是∠ACD和∠BAC的平分线的交点,若AC=6,S△AOC=6则AB与CD之间的距离是( )
如图,已知AB∥CD,O是∠ACD和∠BAC的平分线的交点,若AC=6,S△AOC=6则AB与CD之间的距离是( )
 如图,已知AB∥CD,O是∠ACD和∠BAC的平分线的交点,若AC=6,S△AOC=6则AB与CD之间的距离是( )
如图,已知AB∥CD,O是∠ACD和∠BAC的平分线的交点,若AC=6,S△AOC=6则AB与CD之间的距离是( )| A. | 1cm | B. | 2cm | C. | 3cm | D. | 4cm |
19.下列函数是反比例函数的是( )
| A. | y=x | B. | $y=\frac{-8}{x}$ | C. | y=kx-1 | D. | $y=\frac{8}{x^2}$ |
20.菱形具有而平行四边形不具有的性质是( )
| A. | 内角和是360° | B. | 对角相等 | C. | 对边平行且相等 | D. | 对角线互相垂直 |
 已知△ABC和直线l,作出△ABC关于直线l的对称图形.
已知△ABC和直线l,作出△ABC关于直线l的对称图形.