题目内容
如图,在△ 中,
中, ,以
,以 为直径的⊙O分别交
为直径的⊙O分别交 于点
于点 , 点
, 点 在
在 的延长线上,且
的延长线上,且 ∠
∠
 ∠
∠ 。
。
【小题1】(1) 求证:AB⊥BF
【小题2】(2) 若 sin∠CBF=
sin∠CBF= , 求BC和BF的长。
, 求BC和BF的长。
【小题1】(1)证明:连结AE.
∵AB是⊙O的直径,
∴∠AEB=90º
∴∠1+∠2=90º 
∵AB="AC "
∴∠1= ∠CAB
∠CAB
∵∠CBF= ∠CAB
∠CAB
∴∠1=∠CBF
∴∠CBF+∠2=90º
即∠ABF=90º
∴AB⊥BF …………2分
【小题2】(2) 解:过点C作CG⊥AB于点G.
∵sin∠CBF= ,∠1=∠CBF,
,∠1=∠CBF,
∴sin∠1= ,
,
∵∠AEB=90º,AB=5,
∴BE=AB·sin∠1= ,
,
∵AB="AC," ∠AEB=90º,
∴BC=2BE=2
在Rt△ABE中,由勾股定理得AE=
∴sin∠2= ,cos∠2=
,cos∠2= .
.
在Rt△CBG中,可求得 GC=4,GB=2
∴AG=3.
∵GC∥BF,
∴△AGC∽△ABF
∴ ∴BF=
∴BF= …………5分
…………5分
解析

练习册系列答案
相关题目
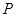 为圆心,1为半径作
为圆心,1为半径作 .
.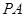 ,若
,若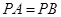 ,试判断
,试判断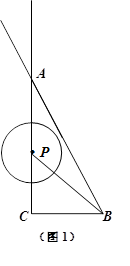
 为圆心,1为半径作
为圆心,1为半径作 .
. ,若
,若 ,试判断
,试判断
 中
中 ,
, ,已知
,已知 ,点
,点 为
为 边上的动点,连接
边上的动点,连接 ,以
,以 为半径的⊙
为半径的⊙ 于点
于点 ,交射线
,交射线 ,交射线
,交射线 ,连接
,连接 .
.
 的长.
的长. 时,求
时,求 的长.
的长. 时,求⊙
时,求⊙ 时,求⊙
时,求⊙ 中,半径长
中,半径长 ,
, ;以
;以 为直径作半圆
为直径作半圆 ,点
,点 是弧
是弧 上的一个动点,
上的一个动点, 与半圆
与半圆 ,
, ⊥
⊥ ,
, 交于点
交于点 ,连结
,连结 .
.
 ;
; ,
,  ,试求
,试求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 上,当
上,当 ∽
∽ 时,求线段
时,求线段 的长度.
的长度.  中
中 ,
, ,已知
,已知 ,点
,点 为
为 边上的动点,连接
边上的动点,连接 ,以
,以 为半径的⊙
为半径的⊙ 于点
于点 ,交射线
,交射线 ,交射线
,交射线 ,连接
,连接 .
.
 的长.
的长. 时,求
时,求 的长.
的长. 时,求⊙
时,求⊙ 时,求⊙
时,求⊙