题目内容
【题目】如图①,将直角梯形![]() 放在平面直角坐标系中,已知
放在平面直角坐标系中,已知![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连结
,连结![]() .
.

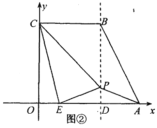
(1)求证:![]() ;
;
(2)如图②,过点![]() 作
作![]() 轴于
轴于![]() ,点
,点![]() 在直线
在直线![]() 上运动,连结
上运动,连结![]() 和
和![]() .
.
①当![]() 的周长最短时,求点
的周长最短时,求点![]() 的坐标;
的坐标;
②如果点![]() 在
在![]() 轴上方,且满足
轴上方,且满足![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①![]() ;②
;②![]() 或8
或8
【解析】
(1)先由已知条件及勾股定理求出AE=4,AB=![]() ,得到
,得到![]() ,又∠OAB=∠BAE,根据两边对应成比例且夹角相等的两三角形相似证明△OAB∽△BAE,得出∠AOB=∠ABE,再由两直线平行,内错角相等得出∠OBC=∠AOB,从而证明∠OBC=∠ABE;
,又∠OAB=∠BAE,根据两边对应成比例且夹角相等的两三角形相似证明△OAB∽△BAE,得出∠AOB=∠ABE,再由两直线平行,内错角相等得出∠OBC=∠AOB,从而证明∠OBC=∠ABE;
(2)①由于CE为定长,所以当PC+PE最短时,△PCE的周长最短,而E与A关于BD对称,故连接AC,交BD于P,即当点C、P、A三点共线时,△PCE的周长最短.由PD∥OC,得出![]() ,求出PD的值,从而得到点P的坐标;
,求出PD的值,从而得到点P的坐标;
②由于点P在x轴上方,BD=4,所以分两种情况:0<PD≤4与PD>4.设PD=t,先用含t的代数式分别表示S△CEP与S△ABP,再根据S△CEP:S△ABP=2:1,即可求出DP的长.
解:(1)由题意可得:
∵OC=4,BC=3,∠OCB=90°,
∴OB=5.
∵OA=5,OE=1,
∴AE=4,AB=![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①∵BD⊥x轴,ED=AD=2,
∴E与A关于BD对称,
当点![]() 共线时,
共线时,![]() 的周长最短.
的周长最短.
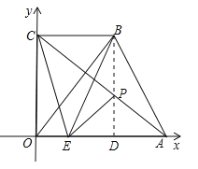
∵![]() ,
,
∴![]() ,即
,即![]()
∴![]()
∴![]() .
.
②设![]() ,
,
当![]() 时,如图:
时,如图:
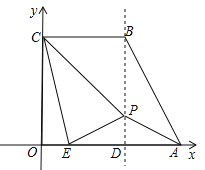
∵![]() 梯
梯![]()
![]() ,
,
![]() ;
;
又∵![]() .
.
∴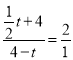 ,
,
∴![]() ;
;
当![]() 时,如图:
时,如图:
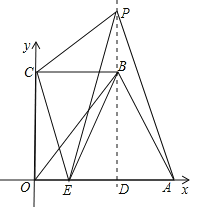
∵![]() ,
,![]() ,
,
∴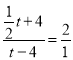
![]() .
.
![]() .
.
∴所求DP的长为![]() 或8.
或8.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目