题目内容
已知,矩形ABCD,AB=4,BE、CF分别平分∠ABC、∠BCD,交AD于E、F,BE、CF相交于G点,EG=
,BC的长为 .
| ||
| 2 |
考点:矩形的性质
专题:
分析:根据矩形的性质得出∠A=∠D=∠ABC=∠DCB=90°,AD∥BC,求出AE=AB=4,根据勾股定理求出EF,求出BE,求出BG,证相似得出比例式,代入求出即可.
解答:
解:∵四边形ABCD是矩形,
∴∠A=∠D=∠ABC=∠DCB=90°,AD∥BC,
∴∠AEB=∠EBC,∠DFC=∠FCB,
∵BE、CF分别平分∠ABC、∠BCD,
∴∠ABE=∠EBC=45°,∠DCF=∠FCB=45°,
∴∠AEB=∠DFC=45°,
∴∠AEB=∠ABE,∠DFC=∠DCF,∠FGE=90°,
∴AE=AB=4,
∵EG=
=FG,
∴由勾股定理得:EF=
=1,BE=
=
=4
,
∴BG=4
-
=
,
∵AD∥BC,
∴△FGE∽△CGB,
∴
=
,
∴
=
,
∴BC=7.
故答案为:7.

解:∵四边形ABCD是矩形,
∴∠A=∠D=∠ABC=∠DCB=90°,AD∥BC,
∴∠AEB=∠EBC,∠DFC=∠FCB,
∵BE、CF分别平分∠ABC、∠BCD,
∴∠ABE=∠EBC=45°,∠DCF=∠FCB=45°,
∴∠AEB=∠DFC=45°,
∴∠AEB=∠ABE,∠DFC=∠DCF,∠FGE=90°,
∴AE=AB=4,
∵EG=
| ||
| 2 |
∴由勾股定理得:EF=
(
|
| AB2+AE2 |
| 42+42 |
| 2 |
∴BG=4
| 2 |
| ||
| 2 |
7
| ||
| 2 |
∵AD∥BC,
∴△FGE∽△CGB,
∴
| EF |
| BC |
| EG |
| BG |
∴
| 1 |
| BC |
| ||||
|
∴BC=7.
故答案为:7.
点评:本题考查了勾股定理,矩形的性质,相似三角形的性质和判定的应用,解此题的关键是求出EF、BG的长和根据相似得出比例式,题目比较好,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在△ABC中,AB=AC,∠BAC=90°,分别从点B、C向过A点的直线作垂线,垂足为M、N,若BM=4,AC=5,求线段MN的长.
如图,在△ABC中,AB=AC,∠BAC=90°,分别从点B、C向过A点的直线作垂线,垂足为M、N,若BM=4,AC=5,求线段MN的长. 已知∠AOB,用直尺和圆规作图:
已知∠AOB,用直尺和圆规作图: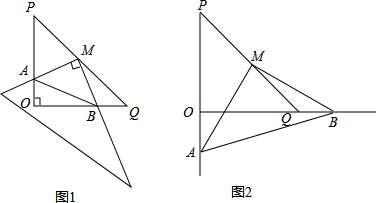
 四边形ABCD是正方形,BE∥CG,∠AEB=60°,BC=CH=2
四边形ABCD是正方形,BE∥CG,∠AEB=60°,BC=CH=2