题目内容
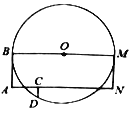
【题目】如图,![]() 是
是![]() 的直径,四边形
的直径,四边形![]() 是矩形,
是矩形,![]() 是
是![]() 上的点,
上的点,![]() ,与
,与![]() 交于点
交于点![]() ,己知
,己知![]() ,
,![]() 的半径为30.
的半径为30.
(1)求![]() 的长.
的长.
(2)连接![]() ,若将扇形
,若将扇形![]() 卷成一个圆锥,求这个圆锥底面半径的长.
卷成一个圆锥,求这个圆锥底面半径的长.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用矩形的性质以及锐角三角形函数关系,得出cos∠EOD的值进而求出∠EOD的度数,再利用弧长公式求出即可;
(2)设圆锥底面半径为r,结合OB=OD=30,∠BOD=60°,根据扇形弧长和圆锥底面周长的关系得出方程,解之即可.
(1)解:连接OD,BD,延长DC交BM于点E,
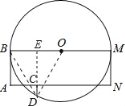
∵BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上一点,DC⊥AN,
∴DE⊥BO,
∵AC=15,
∴BE=EO=15,
∵DO=30,
∴![]() ,
,
∴∠EOD=60°,
∴![]() ;
;
(2)∵OB=OD=30,∠BOD=60°,设圆锥底面半径为r,
由题意可得:![]() ,
,
解得:![]() .
.

练习册系列答案
相关题目