��Ŀ����
��ͼ��ʾ���ھ���ABCD�У�AB=6��AD=2
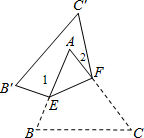
����P�DZ�BC�ϵĶ��㣨��P�����B��C�غϣ�������P��ֱ��PQ��BD����CD����Q�㣬�ٰѡ�PQC���Ŷ�ֱ��PQ���ۣ���C�Ķ�Ӧ����R�㣮��CP=x����PQR�����ABCD�ص����ֵ����Ϊy��
��1�����CPQ�Ķ�����
��2����xȡ��ֵʱ����R���ھ���ABCD�ı�AB�ϣ�
��3������R�ھ���ABCD�ⲿʱ����y��x�ĺ�����ϵʽ�������ʱ����ֵy��ȡֵ��Χ��


| 3 |
��1�����CPQ�Ķ�����
��2����xȡ��ֵʱ����R���ھ���ABCD�ı�AB�ϣ�
��3������R�ھ���ABCD�ⲿʱ����y��x�ĺ�����ϵʽ�������ʱ����ֵy��ȡֵ��Χ��


��1�����ı���ABCD�Ǿ��Σ�
��AB=CD��AD=BC��
��AB=6��AD=2
����C=90�㣬
��CD=6��BC=2
��
��tan��CDB=
=
��
���CDB=30�㣬��CBD=60�㣻
��PQ��BD��
���CPQ=��CBD=60�㣻
��2����ͼ������ԳƵ�����֪����RPQ�ա�CPQ��
���RPQ=��CPQ��RP=CP��
�ɣ�1��֪����CPQ=60�㣬
���RPQ=��CPQ=60�㣻
���RPB=60�㣬
��RP=2BP��
��CP=x��
��RP=x��PB=2
-x��
�ڡ�RPB�У��������⣬�ã�2��2
-x��=x�����x=
��
��3����R�ھ���ABCD���ⲿʱ��
��x��2
��
��Rt��PFB�У��ߡ�RPB=60�㣬
��PF=2BP=2��2
-x����
�֡�RP=CP=x��
��RF=RP-PF=3x-4
��
��Rt��ERF�У��ߡ�EFR=��PFB=30�㣬
��ER=
x-4��
��S��ERF=
ER��FR=
x2-12x+8
��
��y=S��RPQ-S��ERF��
�൱
��x��2
ʱ��y=-
x2+12x-8
��
��
��y��4
��
��AB=CD��AD=BC��
��AB=6��AD=2
| 3 |
��CD=6��BC=2
| 3 |
��tan��CDB=
| BC |
| CD |
| ||
| 3 |
���CDB=30�㣬��CBD=60�㣻
��PQ��BD��
���CPQ=��CBD=60�㣻
��2����ͼ������ԳƵ�����֪����RPQ�ա�CPQ��
���RPQ=��CPQ��RP=CP��
�ɣ�1��֪����CPQ=60�㣬
���RPQ=��CPQ=60�㣻
���RPB=60�㣬
��RP=2BP��
��CP=x��
��RP=x��PB=2
| 3 |
�ڡ�RPB�У��������⣬�ã�2��2
| 3 |
4
| ||
| 3 |
��3����R�ھ���ABCD���ⲿʱ��
| 4 |
| 3 |
| 3 |
| 3 |
��Rt��PFB�У��ߡ�RPB=60�㣬
��PF=2BP=2��2
| 3 |
�֡�RP=CP=x��
��RF=RP-PF=3x-4
| 3 |
��Rt��ERF�У��ߡ�EFR=��PFB=30�㣬
��ER=
| 3 |
��S��ERF=
| 1 |
| 2 |
3
| ||
| 2 |
| 3 |
��y=S��RPQ-S��ERF��
�൱
| 4 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
��
8
| ||
| 3 |
| 3 |

��ϰ��ϵ�д�
�����Ŀ

 ���ۣ�ʹ�õ�A����EF��H�ϣ���ͼ��2�������ۺ۽�AE�ڵ�G����EG�ij��ȣ�
���ۣ�ʹ�õ�A����EF��H�ϣ���ͼ��2�������ۺ۽�AE�ڵ�G����EG�ij��ȣ�