题目内容

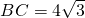已知如图，在矩形ABCD中，AE⊥BD，垂足为E，∠ADB=30°且 $数学公式$ ，求△ECD的面积．

解：∵矩形ABCD，
∴AD=BC=4 $\text{[math]}$ ，
∠DAB=90°=∠ADC，
∵∠ADB=30°，
由勾股定理得：3AB²=AD²= $\text{[math]}$ ，
解得：AB=4，
过E作FE⊥AD于F，EN⊥CD于N，
∵∠ADC=90°，
∴∠EFD=∠END=∠ADC=90°，
∴四边形EFDN是矩形，
∴EF=DN，DF=EN，
在△ADE中，由勾股定理得：AE=2 $\text{[math]}$ ，DE=6，
根据三角形的面积公式得：4 $\text{[math]}$ EF=2 $\text{[math]}$ ×6，
解得：EF=3，
由勾股定理得：DF= $\text{[math]}$ =3 $\text{[math]}$ =EN，
∴△ECD的面积是 $\text{[math]}$ DC•EN= $\text{[math]}$ ×4×3 $\text{[math]}$ =6 $\text{[math]}$ ，
答：△ECD的面积是6 $\text{[math]}$ ．
分析：由矩形ABCD，得到AD=BC=4 $\text{[math]}$ ，由勾股定理得到3AB²=AD²= $\text{[math]}$ ，求出AB=4，过E作FE⊥AD于F，EN⊥CD于N，证四边形EFDN是矩形，推出EF=DN，DF=EN，由勾股定理求出AE=2 $\text{[math]}$ ，DE=6，根据三角形的面积公式得到4 $\text{[math]}$ EF=2 $\text{[math]}$ ×6，求出EF，由勾股定理求出DF、EN的长根据△ECD的面积 $\text{[math]}$ DC•EN求出即可．
点评：本题主要考查对矩形的性质和判定，勾股定理，三角形的面积，含30度角的直角三角形等知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键．