��Ŀ����
��2012•����һģ����ͼ����֪������y=ax2+bx+c���� A��0��4����B��4��0����C��-1��0�����㣮����A�� ��ֱ��y���ֱ��l��������������һ����P������P��ֱ��PQƽ����y�ύֱ��l�ڵ�Q������AP��
��ֱ��y���ֱ��l��������������һ����P������P��ֱ��PQƽ����y�ύֱ��l�ڵ�Q������AP��
��1����������y=ax2+bx+c�Ľ���ʽ��
��2���Ƿ���ڵ�P��ʹ����A��P��Q���㹹�ɵ����������AOC���ƣ�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3������Pλ��������y=ax2+bx+c�ĶԳ�����Ҳ࣮������APQ��AP���ۣ���Q�Ķ�Ӧ��Ϊ��M����M������������ʱֱ��AP�Ľ���ʽ��
 ��ֱ��y���ֱ��l��������������һ����P������P��ֱ��PQƽ����y�ύֱ��l�ڵ�Q������AP��
��ֱ��y���ֱ��l��������������һ����P������P��ֱ��PQƽ����y�ύֱ��l�ڵ�Q������AP����1����������y=ax2+bx+c�Ľ���ʽ��
��2���Ƿ���ڵ�P��ʹ����A��P��Q���㹹�ɵ����������AOC���ƣ�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3������Pλ��������y=ax2+bx+c�ĶԳ�����Ҳ࣮������APQ��AP���ۣ���Q�Ķ�Ӧ��Ϊ��M����M������������ʱֱ��AP�Ľ���ʽ��
��������1����A��0��4����B��4��0����C��-1��0���ֱ����������y=ax2+bx+c���г������飬���������������ʽ��
��2����P��l�·�ʱ�����AOC�ס�AQP����AOC�ס�PQA���������������ε����ʣ��б���ʽ�����������ꣻ��P��l�Ϸ�ʱ�����AOC�ס�AQP����AOC�ס�PQA���������������ε����ʣ��б���ʽ�����������ꣻ
��3����������ͼ�Σ��������������ƣ����P�����꣬�����ô���ϵ���������������ʽ��
��2����P��l�·�ʱ�����AOC�ס�AQP����AOC�ס�PQA���������������ε����ʣ��б���ʽ�����������ꣻ��P��l�Ϸ�ʱ�����AOC�ס�AQP����AOC�ס�PQA���������������ε����ʣ��б���ʽ�����������ꣻ
��3����������ͼ�Σ��������������ƣ����P�����꣬�����ô���ϵ���������������ʽ��
����⣺��1����A��0��4����B��4��0����C��-1��0���ֱ����������y=ax2+bx+c�ã�
��
���
����������ʽΪy=-x2+3x+4��
��2��P��l�·�ʱ����١�AOC�ס�AQP��
=
��
��
=
��
����y=-x2+3x+4��
����
=
��
���x=0����ȥ����x=
����ʱ��y=
��P��������
��
����
�ڡ�AOC�ס�PQA��
=
��
��
=
��
����y=-x2+3x+4��
����
=
��
��ã�x=0����ȥ����x=7��P������Ϊ��7��-24����
��P��l�Ϸ�ʱ�����AOC�ס�PQA��
=
��
��
=
��
��y=-x2+3x+4��
��
=
��
��ã�x=0����ȥ����x=-1��P������Ϊ��-1��0����
�ܡ�AOC�ס�AQP��
=
����
=
��
=
��
��ã�x=0����ȥ����x=
��P��������
��
����
��3����ͼ��1�������ԳƵ�M��y�ᣬ���PAQ=45�㣬
��AP����ʽΪy=kx+b����k=1��-1��
��k=1ʱ����A��0��4�������y=x+4��
��k=-1ʱ����A��0��4�������y=-x+4��
��ʱP�ڶԳ����Ҳ࣬�������⣬
��y=x+4����y=-x+4��
���Q��x��4����P��x��-x2+3x+4������PQ=x2-3x=PM��
�ߡ�AEM�ס�MFP��
����
=
��
��ME=OA=4��AM=AQ=x��PM=PQ=x2-3x��
��
=
��
��ã�PF=4x-12��
��OM=��4x-12��-x=3x-12��
Rt��AOM�У��ɹ��ɶ�����OM2+OA2=AM2��
�ࣨ3x-12��2+42=x2�����x1=4��x2=5�����������߶Գ�����Ҳ࣬
�ʵ�P������Ϊ��4��0����5��-6����
��һ�κ�������ʽΪy=kx+b��
�ѣ�0��4����4��0���ֱ�������ʽ��
��
���
��
��������ʽΪy=-x+4��
�ѣ�0��4����5��-6���ֱ�������ʽ��
��
���
��
��������ʽΪy=-2x+4��
������������������ʽΪy=x+4��y=-x+4��y=-2x+4��
|
���
|
��2��P��l�·�ʱ����١�AOC�ס�AQP��
| AO |
| AQ |
| CO |
| PQ |
��
| 4 |
| x |
| 1 |
| 4-y |
����y=-x2+3x+4��
����
| 4 |
| x |
| 1 |
| 4-(-x2+3x+4) |
���x=0����ȥ����x=
| 13 |
| 4 |
| 51 |
| 16 |
| 13 |
| 4 |
| 51 |
| 16 |
�ڡ�AOC�ס�PQA��
| AQ |
| CO |
| PQ |
| AO |
��
| x |
| 1 |
| 4-y |
| 4 |
����y=-x2+3x+4��
����
| x |
| 1 |
| 4-(-x2+3x+4) |
| 4 |
��ã�x=0����ȥ����x=7��P������Ϊ��7��-24����
��P��l�Ϸ�ʱ�����AOC�ס�PQA��
| AQ |
| CO |
| PQ |
| AO |
��
| x |
| 1 |
| y-4 |
| 4 |
��y=-x2+3x+4��
��
| x |
| 1 |
| -x2+3x+4-4 |
| 4 |
��ã�x=0����ȥ����x=-1��P������Ϊ��-1��0����
�ܡ�AOC�ס�AQP��
| AO |
| AQ |
| CO |
| PQ |
| 4 |
| x |
| 1 |
| y-4 |
��
| 4 |
| x |
| 1 |
| -x2+3x+4-4 |
��ã�x=0����ȥ����x=
| 11 |
| 4 |
| 11 |
| 4 |
| 75 |
| 16 |
��3����ͼ��1�������ԳƵ�M��y�ᣬ���PAQ=45�㣬

��AP����ʽΪy=kx+b����k=1��-1��
��k=1ʱ����A��0��4�������y=x+4��
��k=-1ʱ����A��0��4�������y=-x+4��
��ʱP�ڶԳ����Ҳ࣬�������⣬
��y=x+4����y=-x+4��
���Q��x��4����P��x��-x2+3x+4������PQ=x2-3x=PM��
�ߡ�AEM�ס�MFP��
����
| AM |
| ME |
| MP |
| PF |
��ME=OA=4��AM=AQ=x��PM=PQ=x2-3x��
��
| x |
| 4 |
| x2-3x |
| PF |
��ã�PF=4x-12��
��OM=��4x-12��-x=3x-12��
Rt��AOM�У��ɹ��ɶ�����OM2+OA2=AM2��
�ࣨ3x-12��2+42=x2�����x1=4��x2=5�����������߶Գ�����Ҳ࣬
�ʵ�P������Ϊ��4��0����5��-6����

��һ�κ�������ʽΪy=kx+b��
�ѣ�0��4����4��0���ֱ�������ʽ��
|
���
|
��������ʽΪy=-x+4��
�ѣ�0��4����5��-6���ֱ�������ʽ��
|
���
|
��������ʽΪy=-2x+4��
������������������ʽΪy=x+4��y=-x+4��y=-2x+4��
���������⿼���˶��κ�������ʽ�������κ�������ʽ�����������ε����ʡ����۱任������ϵ������һ�κ�������ʽ�ȣ���Ŀ���۸��ӣ��漰֪ʶ��㣬ּ�ڿ�����˼ά������

��ϰ��ϵ�д�
 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
�����Ŀ
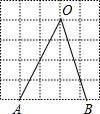 ��2012•����һģ�������������У���AOB��ͼ���ã���cos��AOB��ֵΪ��������
��2012•����һģ�������������У���AOB��ͼ���ã���cos��AOB��ֵΪ��������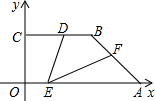 ��2012•����һģ����ͼ��ֱ������OABC��ֱ�Ƕ���������ԭ�㣬��OA��OC�ֱ���X�ᣬy����������ϣ�OA��BC��D��BC��һ�㣬
��2012•����һģ����ͼ��ֱ������OABC��ֱ�Ƕ���������ԭ�㣬��OA��OC�ֱ���X�ᣬy����������ϣ�OA��BC��D��BC��һ�㣬 ��2012•����һģ����ͼ����ֵת������ʾ��ͼ��С���������Ӧ��ϵ������y��x�ĺ���ͼ��
��2012•����һģ����ͼ����ֵת������ʾ��ͼ��С���������Ӧ��ϵ������y��x�ĺ���ͼ��