题目内容
已知|x+| 1 | 2 |
分析:先根据两个非负数的和等于0,则每一个非负数等于0,可求出x、y的值,再化简代数式,把x、y的值代入化简后的代数式计算即可.
解答:解:∵|x+
|≥0,(y-1)2≥0且|x+
|+(y-1)2=0
∴x+
=0,y-1=0,
即x=-
,y=1,
∴原式=4x2y-6xy+2(4xy-2)+x2y+1=4x2y-6xy+8xy-4+x2y+1=5x2y+2xy-3,
当x=-
,y=1时,
原式=
=-
.
| 1 |
| 2 |
| 1 |
| 2 |
∴x+
| 1 |
| 2 |
即x=-
| 1 |
| 2 |
∴原式=4x2y-6xy+2(4xy-2)+x2y+1=4x2y-6xy+8xy-4+x2y+1=5x2y+2xy-3,
当x=-
| 1 |
| 2 |
原式=
|
| 11 |
| 4 |
点评:本题考查了整式的化简求值、非负数的性质.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.

练习册系列答案
相关题目
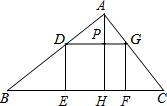 如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.
如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.