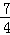题目内容
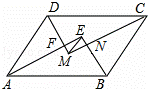
如图,▱ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点H,连接EM.若▱ABCD的周长为42cm,FM=3cm,EF=4cm,则EM= cm,AB= cm.
5. 13
解:∵AE为∠DAB的平分线,
∴∠DAE=∠EAB=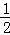 ∠DAB,
∠DAB,
同理:∠ABE=∠CBE=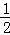 ∠ABC,
∠ABC,
∠BCM=∠DCM=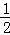 ∠BCD,
∠BCD,
∠CDM=∠ADM=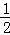 ∠ADC.
∠ADC.
∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,∠ABC=∠ADC,AD=BC.
∴∠DAF=∠BCN,∠ADF=∠CBN.
在△ADF和△CBN中,
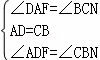 .
.
∴△ADF≌△CBN(ASA).
∴DF=BN.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°.
∴∠EAB+∠EBA=90°.
∴∠AEB=90°.
同理可得:∠AFD=∠DMC=90°.
∴∠EFM=90°.
∵FM=3,EF=4,
∴ME=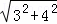 =5(cm).
=5(cm).
∵∠EFM=∠FMN=∠FEN=90°.
∴四边形EFMN是矩形.
∴EN=FM=3.
∵∠DAF=∠EAB,∠AFD=∠AEB,
∴△AFD∽△AEB.
∴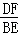 =
=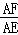 .
.
∴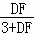 =
=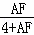 .
.
∴4DF=3AF.
设DF=3k,则AF=4k.
∵∠AFD=90°,
∴AD=5k.
∵∠AEB=90°,AE=4(k+1),BE=3(k+1),
∴AB=5(k+1).
∵2(AB+AD)=42,
∴AB+AD=21.
∴5(k+1)+5k=21.
∴k=1.6.
∴AB=13(cm).
故答案为:5、13.

 阅读快车系列答案
阅读快车系列答案为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
|
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) |
| 甲型挖掘机 | 100 | 60 |
| 乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
已知一组数据:1,2,6,3,3,下列说法正确的是( )
|
| A. | 众数是3 | B. | 中位数是6 | C. | 平均数是4 | D. | 方差是5 |
如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( )

|
| A. |
| B. |
| C. |
| D. |
|
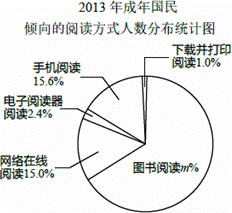
根据某研究院公布的2009~2013年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:
| 2009~2013年成年国民 年人均阅读图书数量统计表 | |
| 年份 | 年人均阅读图书数量(本) |
| 2009 | 3.88 |
| 2010 | 4.12 |
| 2011 | 4.35 |
| 2012 | 4.56 |
| 2013 | 4.78 |
根据以上信息解答下列问题:
(1)直接写出扇形统计图中m的值;
(2)从2009到2013年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估算2014年成年国民年人均阅读图书的数量约为 5 本;
(3)2013年某小区倾向图书阅读的成年国民有990人,若该小区2014年与2013年成年国民的人数基本持平,估算2014年该小区成年国民阅读图书的总数量约为 7500 本.
某茶厂用甲、乙两台分装机分装某种茶叶(每袋茶叶的标准质量为200g).为了监控分装质量,该厂从它们各自分装的茶叶中随机抽取了50袋,测得它们的实际质量分析如下:
|
| 平均数(g) | 方差 |
| 甲分装机 | 200 | 16.23 |
| 乙分装机 | 200 | 5.84 |
则这两台分装机中,分装的茶叶质量更稳定的是 (填“甲”或“乙”).
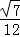 B.
B. 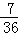
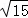 C.
C. 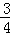
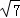 D.
D.