��Ŀ����
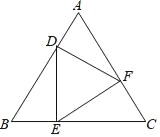
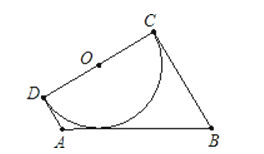
����Ŀ����1����ͼ1����Rt��ABC�У���ACB=90�㣬��A=60�㣬CDƽ����ACB��
��֤��CA+AD=BC��
С��Ϊ��������������������˼��������ADC����ֱ��CD�ĶԳ�ͼ����A��DC��
��CDƽ����ACB����A��������CB�ϣ���CA��=CA��A��D=AD����ˣ�Ҫ֤������ת��ΪֻҪ֤A��D=A��B�������С����˼��д��������������֤�����̣�
��2�����գ�1����С����˼������������������⣺
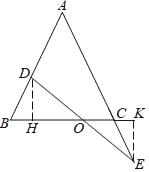
��ͼ3�����ı���ABCD�У�ACƽ����BAD��BC=CD=10��AC=17��AD=9����AB�ij���

���𰸡���1������������2��21.
��������
��1������ADC����CD�ĶԳ�ͼ�Ρ�A��DC����֤��AD=BA�����ɣ�
��2����ͼ������ADC����AC�ĶԳ�ͼ�Ρ�A��DC������C��CE��AB�ڵ�E����D��E=BE����D��E=BE=x����Rt��CEB�У�CE2=CB2��BE2=102��x2����Rt��CEA�У�CE2=AC2��AE2=172����9+x��2���ɴ˹������̼��ɽ�����⣻
��1��֤��������ADC����CD�ĶԳ�ͼ����A��DC��
����ADC����A��DC��
��A��D=AD��C A��=CA����CA��D=��A=60�㣬
��CDƽ����ACB��
��A�������CB��
�ߡ�ACB=90�㣬
���B=90�㩁��A=30�㣬
��CDƽ����ACB��
���ACD=45��
����ACD�У���ADC=180�㩁��A����A CD=75��
���A��DC=��ADC=75�㣬
���A��DB=180�㩁��ADC����A��DC=30�㣬
���A��DB=��B����A��D=A��B��
��CA+AD=CA��+A��D=C A��+A��B=CB��
��2����ͼ������ADC����AC�ĶԳ�ͼ����A��DC��
����ADC����A��DC,
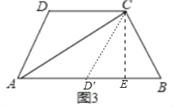
��D��A=DA=9��D��C=DC=10��
��ACƽ����BAD����D�������AB�ϣ�
��BC=10����D��C=BC��
����C��CE��AB�ڵ�E����D��E=BE��
��D��E=BE=x��
��Rt��CEB��CE2=CB2��BE2=102��x2��
��Rt��CEA��CE2=AC2��AE2=172����9+x��2��
��102��x2=172����9+x��2��
��ã�x=6��
��AB=AD��+D��E+EB=9+6+6=21��

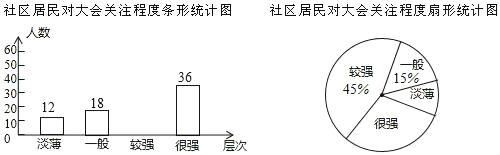
����Ŀ��Ϊ�˽�ijУ�ߣ����꼶ѧ����˯������������ȡ�˸�У�ߣ����꼶����ѧ�����е��飬��֪��ȡ���꼶����꼶��ѧ��������ͬ�����ó������õ����ݻ�������ͳ��ͼ����

��� | ˯��ʱ��x |
A | x��7.5 |
B | 7.5��x��8.5 |
C | 8.5��x��9.5 |
D | 9.5��x��10.5 |
E | x��10.5 |
����ͼ���ṩ����Ϣ���ش��������⣺
��1����ͳ��ͼ�е�a��
��2����ȡ�������У����꼶ѧ��˯��ʱ����C����ж����ˣ�
��3����֪��У���꼶ѧ����755�ˣ����꼶ѧ����785�ˣ����˯��ʱ��x��ʱ�����㣺7.5��x��9.5����˯��ʱ��ϸ��Թ��Ƹ�У�ߡ����꼶ѧ����˯��ʱ��ϸ�Ĺ��ж����ˣ�