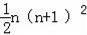题目内容
如图,▱ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:BE=DF.


【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】证明题;压轴题.
【分析】根据平行四边形性质得出AD∥BC,AD=BC,求出DE=BF,DE∥BF,得出四边形DEBF是平行四边形,根据平行四边形的性质推出即可.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
【点评】本题考查了平行四边形的性质和判定的应用,注意:平行四边形的对边平行且相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

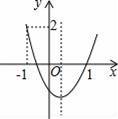
 中,自变量x的取值范围是( )
中,自变量x的取值范围是( ) )
) 


 ,例如2☆3=
,例如2☆3=
 .计算[2☆(﹣4)]×[(﹣4)☆(﹣2)]= .
.计算[2☆(﹣4)]×[(﹣4)☆(﹣2)]= .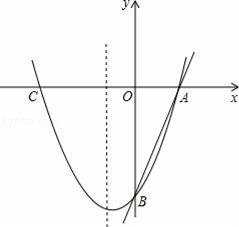

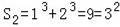
 ;
;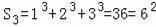
 ;
;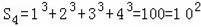
 ;
;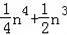
 B.
B.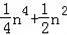

 D.
D.